Cho tam giác \(ABC\) có hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\) thỏa mãn \(\frac{{HD}}{{HA}} = \frac{1}{2}.\)
a) Viết các tỉ số lượng giác của \(\widehat {ABE}.\)
b) Biết \(AH = BD = 2{\rm{\;cm}}\), tính số đo góc \(B\) và độ dài cạnh \(AB,\) độ dài đường cao \(BE\) (làm tròn đến phút đối với số đo góc và làm tròn đến hàng phần mười đối với cm).
c) Chứng minh rằng \(\tan B \cdot \tan C = 3\).
Cho tam giác \(ABC\) có hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\) thỏa mãn \(\frac{{HD}}{{HA}} = \frac{1}{2}.\)
a) Viết các tỉ số lượng giác của \(\widehat {ABE}.\)
b) Biết \(AH = BD = 2{\rm{\;cm}}\), tính số đo góc \(B\) và độ dài cạnh \(AB,\) độ dài đường cao \(BE\) (làm tròn đến phút đối với số đo góc và làm tròn đến hàng phần mười đối với cm).
c) Chứng minh rằng \(\tan B \cdot \tan C = 3\).
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Xét \(\Delta ABE\) vuông tại \(E\) ta có:
\(\sin \widehat {ABE} = \frac{{AE}}{{AB}},\,\,\cos \widehat {ABE} = \frac{{BE}}{{AB}},\) \(\tan \widehat {ABE} = \frac{{AE}}{{BE}},\) \(\cot \widehat {ABE} = \frac{{BE}}{{AE}}.\)
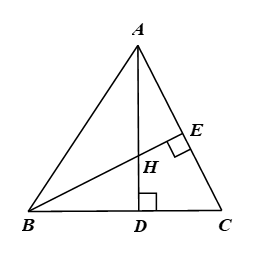
b) Do \(\frac{{HD}}{{HA}} = \frac{1}{2}\) nên \(AH = 2HD\)
Suy ra \(AD = AH + HD = 2HD + HD = 3HD.\)
Ta có \(HD = \frac{1}{2}HA = \frac{1}{2} \cdot 2 = 1{\rm{\;(cm)}}\) và \(AD = 3HD = 3 \cdot 1 = 3{\rm{\;(cm)}}{\rm{.}}\)
Xét \(\Delta ABD\) vuông tại \(D\) ta có:
⦁ \(\tan B = \frac{{AD}}{{BD}} = \frac{3}{2},\) từ đó ta tìm được \(\widehat {B\,} \approx 56^\circ 19'\).
⦁ \(A{B^2} = A{D^2} + B{D^2} = {3^2} + {2^2} = \sqrt {13} {\rm{\;(cm)}}{\rm{.}}\)
Xét \(\Delta HBD\) vuông tại \(D\) ta có:
\(\tan \widehat {HBD} = \frac{{HD}}{{BD}} = \frac{1}{2},\) từ đó ta tìm được \(\widehat {B\,} \approx 26^\circ 34'\).Suy ra \(\widehat {ABE} = \widehat {B\,} - \widehat {HBD} \approx 56^\circ 19' - 26^\circ 34' = 29^\circ 45'\).
Xét \(\Delta ABE\) vuông tại \(E\) ta có:
\(BE = AB \cdot \cos \widehat {ABE} \approx \sqrt {13} \cdot \cos 29^\circ 45' \approx 3,1{\rm{\;(cm)}}{\rm{.}}\)
c) Xét \(\Delta HBD\) và \(\Delta CAD\) có:
\(\widehat {HDB} = \widehat {CDA} = 90^\circ \) và \(\widehat {HBD} = \widehat {CAD}\) (do hai góc này cùng cộng với \(\widehat {C\,}\) bằng \(90^\circ )\)
Do đó (g.g)
Suy ra \(\frac{{HD}}{{CD}} = \frac{{BD}}{{AD}}\) (tỉ số cạnh tương ứng) hay \(BD \cdot CD = HD \cdot AD\).
Xét \(\Delta ACD\) vuông tại \(D\) ta có: \(\tan C = \frac{{AD}}{{CD}}.\)
Khi đó \[\tan B \cdot \tan C = \frac{{AD}}{{BD}} \cdot \frac{{AD}}{{CD}} = \frac{{A{D^2}}}{{BD \cdot CD}} = \frac{{A{D^2}}}{{HD \cdot AD}} = \frac{{AD}}{{HD}} = \frac{{3HD}}{{HD}} = 3.\]
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\) (gam) và \(y\) (gam) lần lượt là khối lượng dung dịch muối ăn với nồng độ \(5\% \) và \(20\% \) cần dùng \(\left( {0 < x < 1\,\,000,\,\,0 < y < 1\,\,000} \right)\).
Theo bài, cần pha trộn hai dung dịch trên để được \(1\,\,000\) g dung dịch muối ăn mới nên ta có phương trình \(x + y = 1\,\,000\). (1)
Khối lượng muối ăn trong \(x\) (gam) dung dịch muối ăn \(5\% \) là \(5\% \cdot x = 0,05x\) (gam).
Khối lượng muối ăn trong \(y\) (gam) dung dịch muối ăn \(20\% \) là \(20\% \cdot x = 0,2x\) (gam).
Khối lượng muối ăn trong \(1\,\,000\) gam dung dịch muối ăn \(14\% \) là \(1\,\,000 \cdot 14\% = 140\) (gam).
Khi đó, ta có phương trình: \(0,05x + 0,2y = 140\). (2)
Từ phương trình (1) và phương trình (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 1\,\,000\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\0,05x + 0,2y = 140\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\)
Nhân hai vế của phương trình (2) với 5, ta được hệ mới là \(\left\{ \begin{array}{l}x + y = 1\,\,000\\0,25x + y = 700\end{array} \right.\)
Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ trên, ta được:
\(0,75x = 300,\) suy ra \(x = 400\) (thỏa mãn).
Thay \(x = 400\) vào phương trình (1), ta được: \(400 + y = 1\,\,000\) suy ra \(y = 600\) (thỏa mãn).
Vậy cần trộn \(400\) gam dung dịch muối ăn \(5\% \) với \(600\) gam dung dịch muối ăn \(20\% \) để được \(1\,\,000\) gam dung dịch muối ăn \(14\% .\)
Lời giải
a) \[\left( {2x + 9} \right)\left( {\frac{2}{3}x - 5} \right) = 0\]
\(2x + 9 = 0\) hoặc \[\frac{2}{3}x - 5 = 0\]
\(2x = - 9\) hoặc \(\frac{2}{3}x = 5\)
\(x = - \frac{9}{2}\) hoặc \(x = \frac{{15}}{2}\).
Vậy phương trình đã cho có hai nghiệm là \(x = - \frac{9}{2};\,\,x = \frac{{15}}{2}\).b) Điều kiện xác định \(x \ne 0;\,\,x \ne 3.\)
\(\frac{{x + 3}}{{x - 3}} = \frac{3}{{{x^2} - 3x}} + \frac{1}{x}\)
\(\frac{{\left( {x + 3} \right)x}}{{x\left( {x - 3} \right)}} = \frac{3}{{x\left( {x - 3} \right)}} + \frac{{x - 3}}{{x\left( {x - 3} \right)}}\)
\(\left( {x + 3} \right)x = 3 + x - 3\)
\({x^2} + 3x = 3 + x - 3\)
\({x^2} + 2x = 0\)
\(x\left( {x + 2} \right) = 0\)
\(x = 0\) hoặc \(x + 2 = 0\)
\(x = 0\) (không thỏa mãn) hoặc \(x = - 2\) (thỏa mãn).
Vậy nghiệm phương trình đã cho là \(x = - 2\).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập