Đường cong trong hình dưới đây là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án \(A\),\(B\),\(C\),\(D\). Hỏi hàm số đó là hàm số nào?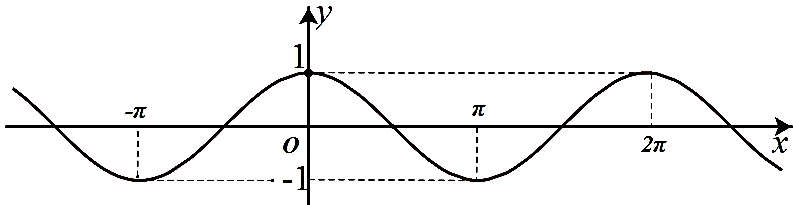
Quảng cáo
Trả lời:
Chọn D
Đồ thị hàm số đi qua điểm \(\left( {\pi ; - 1} \right)\), thay điểm \(\left( {\pi ; - 1} \right)\) vào đáp án D được : \[ - 1 = \cos \left( \pi \right)\] (đúng)
Vậy đồ thị đã cho là đồ thị của hàm số \[y = \cos x\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
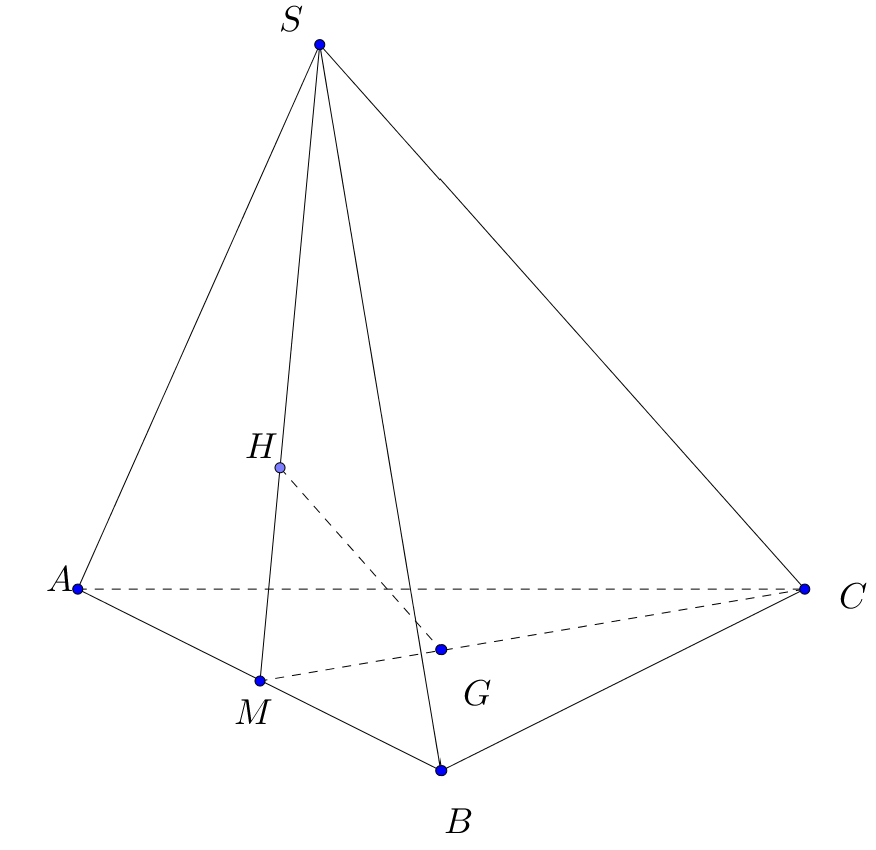
Chọn D
*) \(G\) là trọng tâm tam giác \(ABC\) \( \Rightarrow \frac{{MG}}{{MC}} = \frac{1}{3}\) (1)
*) \(H\) là trọng tâm tam giác \(SAB\) \( \Rightarrow \frac{{MH}}{{MS}} = \frac{1}{3}\) (2)
Từ (1) và (2) suy ra : \(\frac{{MG}}{{MC}} = \frac{{MH}}{{MS}} = \frac{1}{3} \Rightarrow HG{\rm{ // }}SC\) mà \(SC \subset \left( {SAC} \right)\) và \(SC \subset \left( {SBC} \right)\)
Suy ra : \(GH//\left( {SAC} \right)\)và \(\left( {SBC} \right).\)
Câu 2
Lời giải
Chọn A
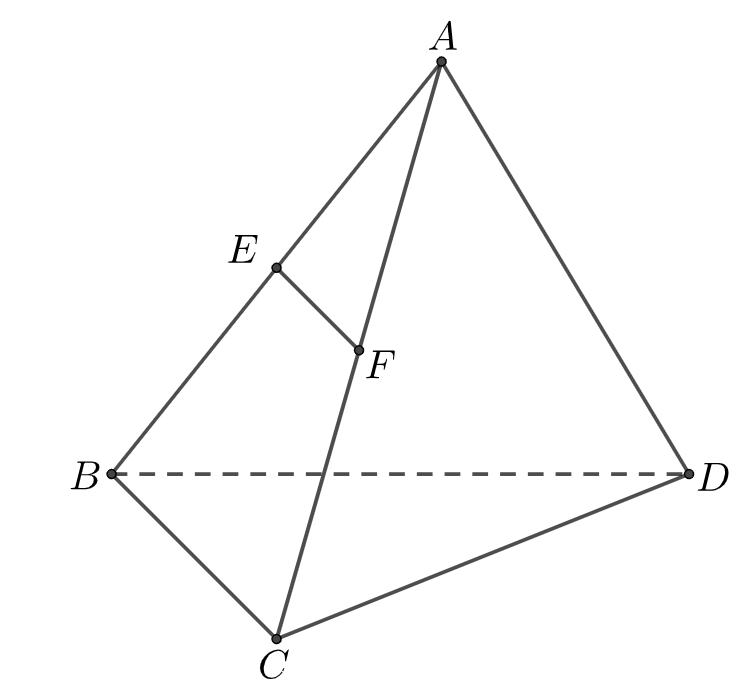
Ta có: \(EF\) là đường trung bình của tam giác \(ABC\) \( \Rightarrow EF\parallel BC\) mà \(BC \subset \left( {BCD} \right)\).
Suy ra:\[EF\parallel (BCD)\]
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.