Cho ba tia\[Ox\], \[Oy\], \[Oz\] vuông góc nhau từng đôi một. Trên \[Ox\], \[Oy\], \[Oz\] lần lượt lấy các điểm\[A\], \[B\], \[C\] sao cho\[OA = OB = OC = a\]. Các mệnh đề sau đúng hay sai?
a) \[O.ABC\] là hình chóp đều.
b) Tam giác \[ABC\] có diện tích \[S = \frac{{{a^2}\sqrt 3 }}{2}\].
c) Tam giác \[ABC\] có chu vi \[2p = \frac{{3a\sqrt 2 }}{2}\].
Quảng cáo
Trả lời:
|
a) Đúng |
b) Đúng |
c) Sai |
d) Đúng |
+ Áp dụng định lý Pytago trong tam giác \[OAB\] vuông tại \[O\] ta có:
\[A{B^2} = O{A^2} + O{B^2} = {a^2} + {a^2} = 2{a^2}\] \[ \Rightarrow AB = a\sqrt 2 \].
Hoàn toàn tương tự ta tính được \[BC = AC = a\sqrt 2 \].
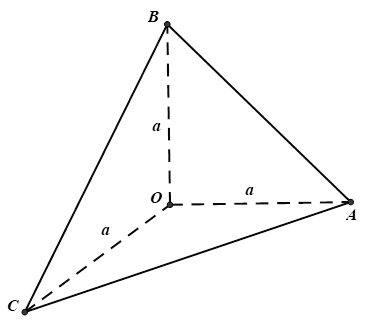
\[ \Rightarrow \Delta ABC\] là tam giác đều. Mặt khác theo giả thiết \[OA = OB = OC = a\] \[ \Rightarrow \] các mặt bên của hình chóp \[O.ABC\] là các tam giác cân tại \[O\] \[ \Rightarrow O.ABC\] là hình chóp đều \[ \Rightarrow \] đáp án a đúng.
+ Chu vi \[\Delta ABC\] là: \[2p = AB + AC + BC = a\sqrt 2 + a\sqrt 2 + a\sqrt 2 = 3a\sqrt 2 \] \[ \Rightarrow \] đáp án c sai.
+ Nửa chu vi Diện tích \[\Delta ABC\] là: \[p = \frac{{3a\sqrt 2 }}{2}\]. Diện tích \[\Delta ABC\] là:
\[S = \sqrt {\frac{{3a\sqrt 2 }}{2}{{\left( {\frac{{3a\sqrt 2 }}{2} - a\sqrt 2 } \right)}^3}} = \sqrt {\frac{{3a\sqrt 2 }}{2}{{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^3}} = \sqrt {\frac{{3a\sqrt 2 }}{2}.\frac{{2{a^3}\sqrt 2 }}{8}} = \sqrt {\frac{{3{a^4}}}{4}} = \frac{{{a^2}\sqrt 3 }}{2}\] (đvdt).
\[ \Rightarrow \] đáp án b đúng.
+ Dễ chứng minh được \[\left\{ \begin{array}{l}OA \bot \left( {OBC} \right)\\OA \subset \left( {OAB} \right)\\OA \subset \left( {OAC} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\left( {OAB} \right) \bot \left( {OBC} \right)\\\left( {OAC} \right) \bot \left( {OBC} \right)\end{array} \right.\], \[\left\{ \begin{array}{l}OB \bot \left( {OAC} \right)\\OB \subset \left( {OAB} \right)\end{array} \right. \Rightarrow \left( {OAB} \right) \bot \left( {OAC} \right)\].
\[ \Rightarrow \] đáp án d đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Trả lời: \(\frac{{25}}{{39}}\)
Lời giải
Ta có sơ đồ cây như sau:
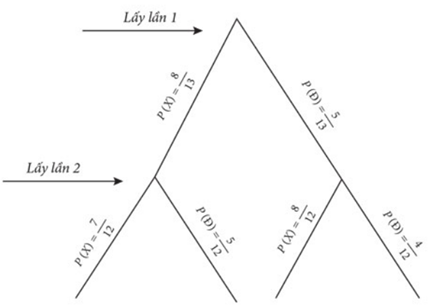
Trong đó: \(X\) là biến cố "Lấy được 1 viên bi màu xanh", Đ là biến cố "Lấy được 1 viên bi màu đỏ".
Xác suất lấy được ít nhất một viên bi đỏ: \(\frac{{25}}{{39}}\).
Lời giải
Trả lời: \(d(AC,SB) = \frac{{3\sqrt {19} }}{{19}}a\)
Lời giải
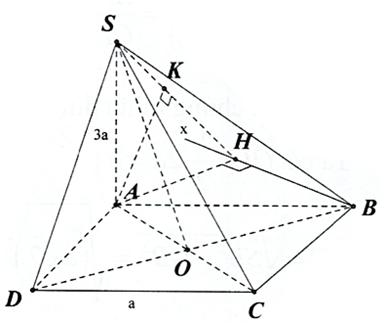
Dựng \(Bx//AC \Rightarrow AC//(SBx)\)
Suy ra \(d(AC,SB) = d(AC,(SBx)) = d(A,(SBx))\)
Dựng và chứng minh được \(d(A,(SBx)) = AK\)
Ta có: \(\Delta AHB\) vuông cân tại \(H\) nên \(AH = \frac{{AB}}{{\sqrt 2 }} = \frac{a}{{\sqrt 2 }}\)
Ta có:
\(AK = \frac{1}{{\sqrt {\frac{1}{{S{A^2}}} + \frac{1}{{A{H^2}}}} }} = \frac{1}{{\sqrt {\frac{1}{{{{(3a)}^2}}} + \frac{1}{{{{\left( {\frac{a}{{\sqrt 2 }}} \right)}^2}}}} }} = \frac{{3\sqrt {19} }}{{19}}a\)
Vậy \(d(AC,SB) = \frac{{3\sqrt {19} }}{{19}}a\).
Câu 3
a) \(P(A) = \frac{4}{9}\)
b) \(P(C) = \frac{1}{9}\)
c) \(P(B) = \frac{4}{9}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(90^\circ \).
B. \(60^\circ \).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\left( {SBC} \right) \bot \left( {SAB} \right)\).
B. \(\left( {SAB} \right) \bot \left( {ABCD} \right)\).
C. \(\left( {SAC} \right) \bot \left( {ABCD} \right)\).
D. \(\left( {SAC} \right) \bot \left( {SAD} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.