Tam giác \(ABC\) có hai đường trung tuyến \(BM,CN\) vuông góc với nhau và có \(BC = 6\), \(\widehat {BAC} = 30^\circ \). Tính diện tích \(\Delta ABC\) (kết quả làm tròn đến hàng phần chục).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
20,8
Lời giải
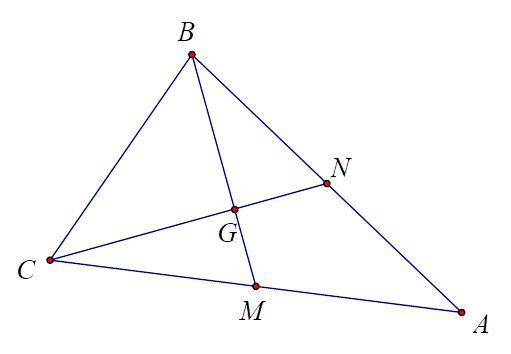
Đặt \(AC = b,AB = c\).
Ta có \(B{C^2} = {b^2} + {c^2} - 2bc\cos A = {b^2} + {c^2} - 2bc\cos 30^\circ = {b^2} + {c^2} - bc\sqrt 3 \Rightarrow bc\sqrt 3 = {b^2} + {c^2} - 36\) (1).
Áp dụng định lí côsin cho tam giác \(ABM\), có \(B{M^2} = {c^2} + \frac{{{b^2}}}{4} - bc\cos A = {c^2} + \frac{{{b^2}}}{4} - \frac{{\sqrt 3 }}{2}bc\)\( \Leftrightarrow B{M^2} = {c^2} + \frac{{{b^2}}}{4} - \frac{{{b^2} + {c^2} - 36}}{2} = \frac{{{c^2}}}{2} - \frac{{{b^2}}}{4} + 18\).
Áp dụng định lí côsin cho tam giác \(ACN\), \(C{N^2} = {b^2} + \frac{{{c^2}}}{4} - \frac{{bc\sqrt 3 }}{2}\)\( = {b^2} + \frac{{{c^2}}}{4} - \frac{{{b^2} + {c^2} - 36}}{2} = \frac{{{b^2}}}{2} - \frac{{{c^2}}}{4} + 18\).
Lại có \(B{G^2} + C{G^2} = 36\)\( \Leftrightarrow \frac{4}{9}\left( {B{M^2} + C{N^2}} \right) = 36\)\( \Leftrightarrow B{M^2} + C{N^2} = 81\)\( \Leftrightarrow \frac{{{c^2}}}{2} - \frac{{{b^2}}}{4} + 18 + \frac{{{b^2}}}{2} - \frac{{{c^2}}}{4} + 18 = 81\)
\( \Leftrightarrow \frac{{{c^2}}}{4} + \frac{{{b^2}}}{4} = 45\)\( \Leftrightarrow {c^2} + {b^2} = 180\) (2).
Từ (1) và (2), suy ra \(bc = 48\sqrt 3 \).
Khi đó \({S_{ABC}} = \frac{1}{2}bc\sin A = \frac{1}{2} \cdot 48\sqrt 3 \cdot \sin 30^\circ = 12\sqrt 3 \approx 20,8\).
Trả lời: 20,8.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Lời giải
\(P = {\cos ^2}1^\circ + {\cos ^2}2^\circ + {\cos ^2}3^\circ + ... + {\cos ^2}178^\circ + {\cos ^2}179^\circ + {\cos ^2}180^\circ \)
\(P = \left( {{{\cos }^2}1^\circ + {{\cos }^2}179^\circ } \right) + \left( {{{\cos }^2}2^\circ + {{\cos }^2}178^\circ } \right) + ... + \left( {{{\cos }^2}89^\circ + {{\cos }^2}91^\circ } \right) + {\cos ^2}90^\circ + {\cos ^2}180^\circ \)
\(P = \left( {{{\cos }^2}1^\circ + {{\cos }^2}1^\circ } \right) + \left( {{{\cos }^2}2^\circ + {{\cos }^2}2^\circ } \right) + ... + \left( {{{\cos }^2}89^\circ + {{\cos }^2}89^\circ } \right) + {\cos ^2}90^\circ + {\cos ^2}180^\circ \)
\[P = 2{\cos ^2}1^\circ + 2{\cos ^2}2^\circ + ... + 2{\cos ^2}89^\circ + {\cos ^2}90^\circ + {\cos ^2}180^\circ \]
\[P = 2\left( {{{\cos }^2}1^\circ + {{\cos }^2}89^\circ } \right) + 2\left( {{{\cos }^2}2^\circ + {{\cos }^2}88^\circ } \right) + ... + 2\left( {{{\cos }^2}44^\circ + {{\cos }^2}46^\circ } \right) + 2{\cos ^2}45^\circ + {\cos ^2}90^\circ + {\cos ^2}180^\circ \]
\[P = 2\left( {{{\cos }^2}1^\circ + {{\sin }^2}1^\circ } \right) + 2\left( {{{\cos }^2}2^\circ + {{\sin }^2}2^\circ } \right) + ... + 2\left( {{{\cos }^2}44^\circ + {{\sin }^2}44^\circ } \right) + 2{\cos ^2}45^\circ + {\cos ^2}90^\circ + {\cos ^2}180^\circ \]
\[P = 2 \cdot 44 + 1 + 1 = 90\].
Trả lời: 90.
Lời giải
Lời giải
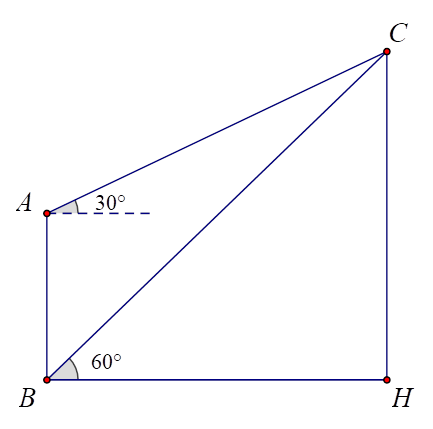
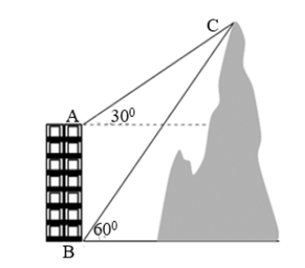
Xét \(\Delta ABC\) có \(\widehat {BAC} = 90^\circ + 30^\circ = 120^\circ \); \(\widehat {ABC} = 90^\circ - 60^\circ = 30^\circ \); \(\widehat {ACB} = 180^\circ - 120^\circ - 30^\circ = 30^\circ \).
Áp dụng định lí sin cho tam giác \(ABC\), có
\(\frac{{AB}}{{\sin C}} = \frac{{BC}}{{\sin A}} \Rightarrow BC = \frac{{AB\sin A}}{{\sin C}} = \frac{{70\sin 120^\circ }}{{\sin 30^\circ }} = 70\sqrt 3 \).
Xét \(\Delta AHC\) có \(CH = BC\sin 60^\circ = 70\sqrt 3 \cdot \sin 60^\circ = 105\).
Vậy ngọn núi cao 105 m.
Trả lời: 105.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
a) Giá trị \(\sin \alpha \cdot \cos \alpha < 0\).
Đúng
Sai
b) Có \(\sin \alpha = \frac{{2\sqrt 2 }}{3}\).
Đúng
Sai
c) Có \(\tan \alpha = \frac{{\sqrt 2 }}{4}\).
Đúng
Sai
d) Giá trị biểu thức \(\frac{{6\sqrt 2 \sin \alpha + 3\cos \alpha }}{{\sqrt 2 \tan \alpha + 2\sqrt 2 \cot \alpha }} = \frac{9}{5}\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập