Thu nhập bình quân đầu người (GDP) của Việt Nam (tính theo USD) trong vòng 5 năm, từ năm 2017 đến năm 2021 (dựa theo số liệu của solieukinhte.com)

Năm	2017	2018	2019	2020	2021
GDP	2 974	3 231	3 425	3 526	3 694

Bảng này xác định một hàm số chỉ sự phụ thuộc của GDP (kí hiệu \(y\)) vào thời gian \(x\)(tính bằng năm). Khẳng định nào sau đây là sai? 

Đáp án đúng là: A

Hàm số \(y = {x^2} + 2mx + 5\) có \(a = 1 > 0\) nên hàm số đạt giá trị nhỏ nhất khi \(x =  - \frac{b}{{2a}} =  - \frac{{2m}}{{2.1}} =  - m\).

Theo bài ra ta có: \(y\left( { - m} \right) = 1 \Leftrightarrow {\left( { - m} \right)^2} + 2m.\left( { - m} \right) + 5 = 1 \Leftrightarrow {m^2} = 4 \Leftrightarrow m =  \pm 2\).

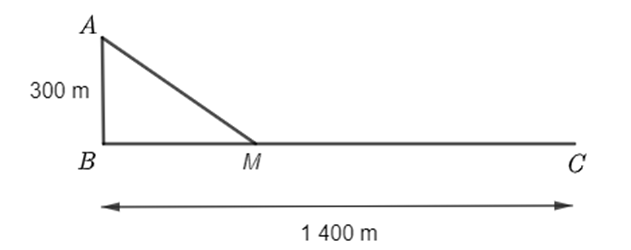
Giả sử \[A\left( {a;0} \right),\,\,B\left( {0;b} \right)\]

Vì \[OA = OB\] nên \[\left| a \right| = \left| b \right| \Leftrightarrow a =  \pm b\]

Phương trình \[AB:\frac{x}{a} + \frac{y}{b} = 1\]

Vì \[M\left( { - 2; - 4} \right) \in AB\] nên \[ - \frac{2}{a} - \frac{4}{b} = 1 & \left( * \right)\]

Ÿ Nếu \[a = b\] thì \[\left( * \right) \Leftrightarrow  - \frac{6}{a} = 1 \Rightarrow a = b =  - 6\]

Vậy phương trình \[AB:\frac{x}{{ - 6}} + \frac{y}{{ - 6}} = 1 \Leftrightarrow x + y + 6 = 0\]

Ÿ Nếu \[a =  - b\] thì \[\left( * \right) \Leftrightarrow  - \frac{2}{a} + \frac{4}{a} = 1 \Rightarrow \frac{2}{a} = 1 \Rightarrow a = 2 \Rightarrow b =  - 2\]

Vậy phương trình \[AB:\frac{x}{2} - \frac{y}{2} = 1 \Leftrightarrow x - y - 2 = 0\].