(2,5 điểm)

Cô Linh chia số tiền   triệu đồng của mình cho hai khoản đầu tư. Sau một năm, tổng số tiền lãi thu được là   triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là  /năm và khoản đầu tư thứ hai là  /năm. Tính số tiền cô Linh đầu tư cho mỗi khoản.

Thay \(x = 9\left( {TM} \right)\) vào biểu thức A, ta có:

\(A = \frac{{\sqrt 9  + 5}}{{2\sqrt 9  - 4}} = \frac{{3 + 5}}{{2.3 - 4}} = \frac{8}{2} = 4\)

Vậy \(A = 4\) khi \(x = 9\).

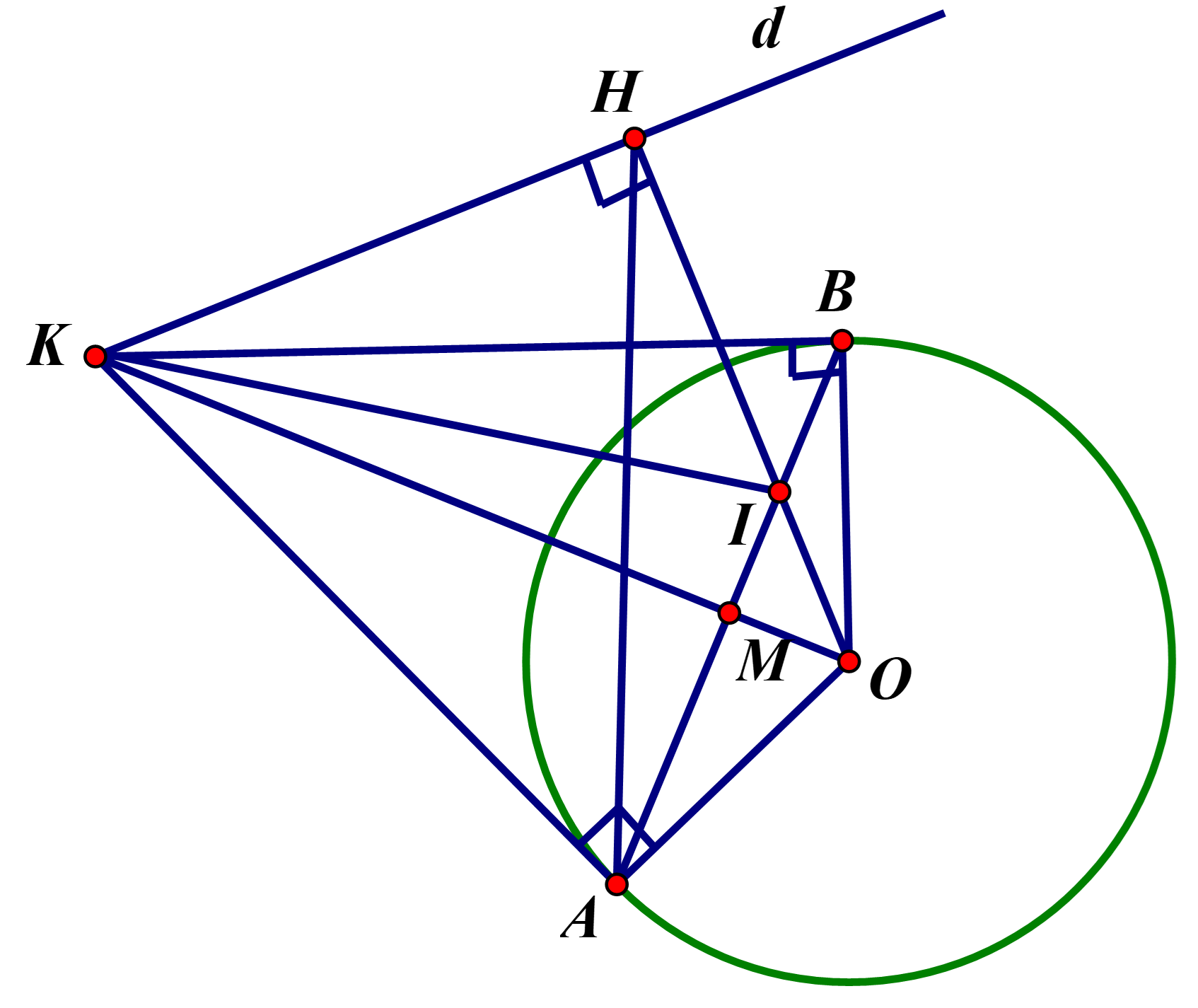
a)  = 900( vì KA là tiếp tuyến của (O) (gt))

 = 900( )

Suy ra tam giác KAO vuông tại A, tam giác KHO vuông tại H

 Nên A, H thuộc đường tròn đường kính OK

Vậy tứ giác \(KAOH\) nội tiếp được trong đường tròn.

b) Các đỉnh \(H,B,A\) cùng nhìn cạnh \(OK\) dưới một góc vuông

 nên năm điểm \(K,A,B,O,H\) cùng thuộc đường tròn đường kính \(OK\) suy ra  \(\widehat {AHI} = \widehat {ABO}\) (hai góc nội tiếp cùng chắn cung \(AO\)).

 Xét tam giác \(IAH\) và tam giác \(IOB\) có:

 \(\widehat {HIA} = \widehat {BIO}\) (đối đỉnh)

và \(\widehat {AHI} = \widehat {ABO}\) ( cmt ).

Do đó .

c) Gọi \(M\) là giao điểm của OK và AB

Theo tính chất tiếp tuyến ta có KA=KB;

Lại có \(OA = OB = R\) nên OK là đường trung trực của AB, suy ra \(AB \bot OK\) tại \(M\) và \(MA = MB\).

Ta có: \(\Delta OMI \sim \Delta OHK\;(g.g)\) suy ra  \(OI = \frac{{OK.OM}}{{OH}} = \frac{{O{A^2}}}{{OH}} = \frac{{{R^2}}}{{OH}} = \frac{{{R^2}}}{{R\sqrt 3 }} = \frac{R}{{\sqrt 3 }}\).

Xét \(\Delta OAK\) vuông tại \(A\), có \(O{A^2} = OM \cdot OK \Leftrightarrow OM = \frac{{O{A^2}}}{{OK}} = \frac{{{R^2}}}{{2R}} = \frac{R}{2}\)

Suy ra \(KM = OK - OM = 2R - \frac{R}{2} = \frac{{3R}}{2}\)

\(A{M^2} = OM \cdot KM = \frac{R}{2} \cdot \frac{{3R}}{2} = \frac{{3{R^2}}}{4} \Rightarrow AM = \frac{{R\sqrt 3 }}{2}\)

Xét \(\Delta OMI\) vuông tại \(M\), có \(MI = \sqrt {O{I^2} - O{M^2}}  = \sqrt {{{\left( {\frac{R}{{\sqrt 3 }}} \right)}^2} - {{\left( {\frac{R}{2}} \right)}^2}}  = \frac{{R\sqrt 3 }}{6}\)

Suy ra \(AI = AM + MI = \frac{{R\sqrt 3 }}{2} + \frac{{R\sqrt 3 }}{6} = \frac{{2R\sqrt 3 }}{3}\)

Diện tích \(\Delta AKI\) là \(S = \frac{1}{2}AI \cdot KM = \frac{1}{2} \cdot \frac{{3R}}{2} \cdot \frac{{2R\sqrt 3 }}{3} = \frac{{{R^2}\sqrt 3 }}{2}\).