(0,5 điểm)
Máng trượt của một cầu trượt cho trẻ em được uốn từ một tấm kim loại có bề rộng \(80\)cm, mặt cắt được mô tả ở hình vẽ dưới đây. Nhà thiết kế khuyến cáo, diện tích của mặt cắt càng lớn thì càng đảm bảo an toàn cho trẻ em.
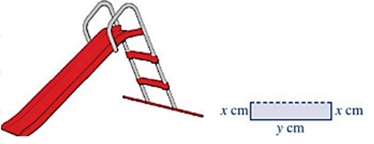
Gọi \(S\) là diện tích mặt cắt máng trượt. Hỏi \(x\) đạt giá trị bao nhiêu thì cầu trượt đảm bảo an toàn nhất cho trẻ em?
(0,5 điểm)
Máng trượt của một cầu trượt cho trẻ em được uốn từ một tấm kim loại có bề rộng \(80\)cm, mặt cắt được mô tả ở hình vẽ dưới đây. Nhà thiết kế khuyến cáo, diện tích của mặt cắt càng lớn thì càng đảm bảo an toàn cho trẻ em.

Gọi \(S\) là diện tích mặt cắt máng trượt. Hỏi \(x\) đạt giá trị bao nhiêu thì cầu trượt đảm bảo an toàn nhất cho trẻ em?
Quảng cáo
Trả lời:
Vì tấm kim loại có bề rộng \(80\)cm nên ta có phương trình: \(2x + y = 80\).
Để có thể thiết kế được máng trượt thì \(x > 0;\,y > 0\) nên \(80 - 2x > 0\) hay \(x < 40\).
Diện tích của mặt máng trượt là: \(S = x.y = x\left( {80 - 2x} \right) = - 2{x^2} + 80x\) với \(0 < x < 40\).
Ta có: \(\)\( - 2{x^2} + 80x = - 2\left( {{x^2} - 40x} \right) = - 2\left( {{x^2} - 2.20.x + {{20}^2} - {{20}^2}} \right)\)
Hay \(S = - 2\left( {{x^2} - 2.20.x + {{20}^2}} \right) + 800 = - 2{\left( {x - 20} \right)^2} + 800\)
Ta thấy: \( - 2{\left( {x - 20} \right)^2} \le 0\) luôn đúng với mọi số thực \(x\).
Suy ra: \( - 2{\left( {x - 20} \right)^2} + 800 \le 800\)
Hay \(S \le 800\). Dấu xảy ra khi \(x = 20\)( thỏa mãn).
Vậy khi \(x = 20\) thì diện tích bề mặt lớn nhất (\(800c{m^2}\)) khi đó thì cầu trượt đảm bảo an toàn nhất cho trẻ em.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Từ bảng tần số trên ta thấy có \(12\) học viên đạt điểm từ \(\left[ {7,5;10} \right)\).
Vậy có 12 học viên xếp loại \(A\).
Lời giải
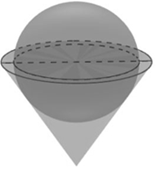
Một bình đựng đầy nước có dạng hình nón (không có
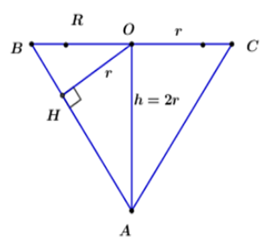
Gọi r là bán kính khối cầu; \(R\) là bán kính khối nón; \(h\) là chiều cao khối nón
Ta có \(h = 2r\) (dm)
Theo đề bài ta có:
Thể tích nửa khối cầu là 18π (dm3)
Suy ra \(r = 3\) (dm) và \(h = 6\) (dm)
Xét tam giác \(OAB\) vuông tại \(O\) có đường cao \(OH\) nên \(R = \frac{{2\sqrt 3 }}{3}r = 2\sqrt 3 \) (dm)
Khi đó thể tích khối nón sẽ là \(24\pi \)(dm3)
Vậy thể tích nước còn lại trong bình là \(6\pi \)(dm3)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.