(1,5 điểm)

Sau một khóa tập huấn, học viên được xếp loại \(A;B;C;D\)theo điểm kiểm tra mà mỗi người đạt được như sau:

Điểm kiểm tra (X)	\(0 \le X < 2,5\)	\(2,5 \le X < 5\)	\(5 \le X < 7,5\)	\(7,5 \le X < 10\)
Xếp loại	\(D\)	\(C\)	\(B\)	\(A\)

Điểm kiểm tra của các học viên được ghi lại ở bảng sau đây:

\(6,5\)	\(1,4\)	\(7,3\)	\(8,4\)	\(4,7\)	\(9,8\)	\(9,9\)	\(6,4\)	\(2,9\)	\(3,1\)
\(4,5\)	\(8,7\)	\(7,8\)	\(5,4\)	\(7,7\)	\(7\)	\(9\)	\(9,4\)	\(7,2\)	\(8,8\)
\(9,2\)	\(1,9\)	\(7,3\)	\(0,5\)	\(4,7\)	\(2,5\)	\(9,6\)	\(6,8\)	\(5,9\)	\(8\)

Hỏi có bao nhiêu học viên xếp loại \(A\)?

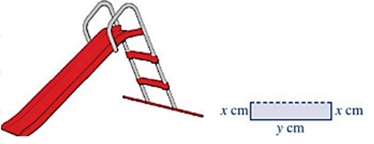
Vì tấm kim loại có bề rộng \(80\)cm nên ta có phương trình: \(2x + y = 80\).

Để có thể thiết kế được máng trượt thì \(x > 0;\,y > 0\) nên \(80 - 2x > 0\) hay \(x < 40\).

Diện tích của mặt máng trượt là: \(S = x.y = x\left( {80 - 2x} \right) =  - 2{x^2} + 80x\) với \(0 < x < 40\).

Ta có: \(\)\( - 2{x^2} + 80x =  - 2\left( {{x^2} - 40x} \right) =  - 2\left( {{x^2} - 2.20.x + {{20}^2} - {{20}^2}} \right)\)

Hay \(S =  - 2\left( {{x^2} - 2.20.x + {{20}^2}} \right) + 800 =  - 2{\left( {x - 20} \right)^2} + 800\)

Ta thấy: \( - 2{\left( {x - 20} \right)^2} \le 0\)  luôn đúng với mọi số thực \(x\).

Suy ra: \( - 2{\left( {x - 20} \right)^2} + 800 \le 800\)

 Hay \(S \le 800\). Dấu   xảy ra khi \(x = 20\)( thỏa mãn).

Vậy khi \(x = 20\) thì diện tích bề mặt lớn nhất (\(800c{m^2}\)) khi đó thì cầu trượt đảm bảo an toàn nhất cho trẻ em.

Gọi số bước chân anh Sơn và chị Hà đi được trong 1 phút lần lượt là x và y \(\left( {x,y \in {\mathbb{N}^*}} \right).\)

Vì nếu cùng đi trong 2 phút thì anh Sơn bước nhiều hơn chị Hà 20 bước nên ta có phương trình \(2x - 2y = 20\)                                                (1).

Vì nếu chị Hà đi trong 5 phút thì lại nhiều hơn anh Sơn đi trong 3 phút là 160 bước từ đó ta có \(5y - 3x = 160\)                                              (2).

Từ (1) và (2) suy ra x = 105 và y = 95.

Vậy                                                       trong một giờ anh Sơn đi được \(105.60 = 6300\)

trong một giờ chị Hà đi được \(95.60 = 5700\).

Do anh Sơn và chị Hà đề ra mục tiêu mỗi ngày một người phải đi bộ ít nhất 6000 bước nên anh Sơn đã đạt được mục tiêu tối thiểu mà mình đề ra, còn chị Hà thì chưa.