(1,5 điểm)
Cho biểu thức \(A = \frac{{x + 2\sqrt x + 5}}{{\sqrt x - 3}}\)(với \(x \ge 0;x \ne 9\)).Tính giá trị của \(A\) khi \(x = 16.\)
Cho biểu thức \(A = \frac{{x + 2\sqrt x + 5}}{{\sqrt x - 3}}\)(với \(x \ge 0;x \ne 9\)).Tính giá trị của \(A\) khi \(x = 16.\)
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 9 !!
Quảng cáo
Trả lời:
Ta có \(x = 16\) (thỏa mãn điều kiện), thay vào biểu thức \(A\) ta có:
\(A = \frac{{16 + 2\sqrt {16} + 5}}{{\sqrt {16} - 3}} = \frac{{29}}{1} = 29\)
Vậy khi \(x = 16\) thì \(A = 29\)
Câu hỏi cùng đoạn
Câu 2:
Cho biểu thức: \(P = \frac{{\sqrt x + 2}}{{\sqrt x + 3}} - \frac{5}{{x + \sqrt x - 6}} - \frac{1}{{\sqrt x - 2}}\) (với \(x \ge 0;x \ne 4\))
a) Chứng minh \(P = \frac{{\sqrt x - 4}}{{\sqrt x - 2}}\).
b) Tìm tất cả các giá trị của \[x\] để \({P^2} > P\).
Cho biểu thức: \(P = \frac{{\sqrt x + 2}}{{\sqrt x + 3}} - \frac{5}{{x + \sqrt x - 6}} - \frac{1}{{\sqrt x - 2}}\) (với \(x \ge 0;x \ne 4\))
a) Chứng minh \(P = \frac{{\sqrt x - 4}}{{\sqrt x - 2}}\).
b) Tìm tất cả các giá trị của \[x\] để \({P^2} > P\).
a) Ta có \(P = \frac{{\sqrt x + 2}}{{\sqrt x + 3}} - \frac{5}{{x + \sqrt x - 6}} - \frac{1}{{\sqrt x - 2}}\)
\( = \frac{{\sqrt x + 2}}{{\sqrt x + 3}} - \frac{5}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 2} \right)}} - \frac{1}{{\sqrt x - 2}}\)
\( = \frac{{\left( {\sqrt x + 2} \right)\left( {\sqrt x - 2} \right) - 5 - \left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 2} \right)}}\)
\( = \frac{{x - 4 - 5 - \sqrt x - 3}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 2} \right)}} = \frac{{x - \sqrt x - 12}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 2} \right)}}\)
\( = \frac{{\left( {\sqrt x - 4} \right)\left( {\sqrt x + 3} \right)}}{{\left( {\sqrt x + 3} \right)\left( {\sqrt x - 2} \right)}} = \frac{{\sqrt x - 4}}{{\sqrt x - 2}}\)
Vậy khi \(x \ge 0;x \ne 4\), thì \(P = \frac{{\sqrt x - 4}}{{\sqrt x - 2}}\)(điều phải chứng minh).
b) Ta có \(P = \frac{{\sqrt x - 4}}{{\sqrt x - 2}}\) với điều kiện \(x \ge 0;x \ne 4\)
+ Để \({P^2} > P\) thì \(P\left( {P - 1} \right) > 0\)
\(\frac{{\sqrt x - 4}}{{\sqrt x - 2}}.\left( {\frac{{\sqrt x - 4}}{{\sqrt x - 2}} - 1} \right) > 0\) hay \(\frac{{ - 2\left( {\sqrt x - 4} \right)}}{{{{\left( {\sqrt x - 2} \right)}^2}}} > 0\)
\( - 2\left( {\sqrt x - 4} \right) > 0\) (vì \({\left( {\sqrt x - 2} \right)^2} > 0\,\,\forall x\) thỏa mãn điều kiện xác định)
\(\begin{array}{l}\sqrt x - 4 < 0\\x < 16\end{array}\)
Kết hợp với điều kiện ta được \(\left\{ \begin{array}{l}0 < x < 16\\x \ne 4\end{array} \right.\)
Vậy khi \(\left\{ \begin{array}{l}0 < x < 16\\x \ne 4\end{array} \right.\) thì \({P^2} > P\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
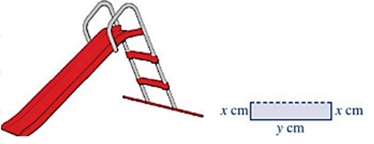
Vì tấm kim loại có bề rộng \(80\)cm nên ta có phương trình: \(2x + y = 80\).
Để có thể thiết kế được máng trượt thì \(x > 0;\,y > 0\) nên \(80 - 2x > 0\) hay \(x < 40\).
Diện tích của mặt máng trượt là: \(S = x.y = x\left( {80 - 2x} \right) = - 2{x^2} + 80x\) với \(0 < x < 40\).
Ta có: \(\)\( - 2{x^2} + 80x = - 2\left( {{x^2} - 40x} \right) = - 2\left( {{x^2} - 2.20.x + {{20}^2} - {{20}^2}} \right)\)
Hay \(S = - 2\left( {{x^2} - 2.20.x + {{20}^2}} \right) + 800 = - 2{\left( {x - 20} \right)^2} + 800\)
Ta thấy: \( - 2{\left( {x - 20} \right)^2} \le 0\) luôn đúng với mọi số thực \(x\).
Suy ra: \( - 2{\left( {x - 20} \right)^2} + 800 \le 800\)
Hay \(S \le 800\). Dấu xảy ra khi \(x = 20\)( thỏa mãn).
Vậy khi \(x = 20\) thì diện tích bề mặt lớn nhất (\(800c{m^2}\)) khi đó thì cầu trượt đảm bảo an toàn nhất cho trẻ em.
Lời giải
Từ bảng tần số trên ta thấy có \(12\) học viên đạt điểm từ \(\left[ {7,5;10} \right)\).
Vậy có 12 học viên xếp loại \(A\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.