(1,5 điểm)
Trong bảng số liệu sau có một số lệu bị điều tra sai. Hãy tìm số liệu đó và sửa cho đúng.
Tần số
\[24\]
\[16\]
\[6\]
\[4\]
Tần số tương đối
\[48\% \]
\[32\% \]
\[15\% \]
\[8\% \]
Trong bảng số liệu sau có một số lệu bị điều tra sai. Hãy tìm số liệu đó và sửa cho đúng.
|
Tần số |
\[24\] |
\[16\] |
\[6\] |
\[4\] |
|
Tần số tương đối |
\[48\% \] |
\[32\% \] |
\[15\% \] |
\[8\% \] |
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 24 !!
Quảng cáo
Trả lời:
Câu hỏi cùng đoạn
Câu 2:
Hình bên dưới mô tả một đĩa tròn bằng bìa cứng được chia làm \[12\]phần bằng nhau và ghi các số \[1,2,3,...,12\]; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.
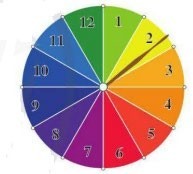
Xét phép thử “Quay đĩa tròn một lần”. Tính xác suất của biến cố D: “Chiếc kim chỉ vào hình
quạt ghi số nguyên tố”.
Hình bên dưới mô tả một đĩa tròn bằng bìa cứng được chia làm \[12\]phần bằng nhau và ghi các số \[1,2,3,...,12\]; chiếc kim được gắn cố định vào trục quay ở tâm của đĩa.

Xét phép thử “Quay đĩa tròn một lần”. Tính xác suất của biến cố D: “Chiếc kim chỉ vào hình
quạt ghi số nguyên tố”.Có \[12\]kết quả có thể của phép thử “Quay đĩa tròn \[1\] lần” là \[1,2,3,...,12\].
Có \[5\] kết quả thuận lợi cho biến cố D: “Chiếc kim chỉ vào hình quạt ghi số nguyên tố”
Vậy xác suất của biến cố D là \[\frac{5}{{12}}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\)(đồng) là giá tiền ban đầu của chiếc ti vi khi chưa khuyến mãi \(\left( {x > 0} \right)\)
Giá tiền của chiếc ti vi sau khi được giảm giá \[10\% \] là: \[x.\left( {1 - 10\% } \right) = 0,9x\](đồng)
Giá tiền của chiếc ti vi sau khi được giảm giá thêm \[5\% \] giá đã giảm do có thẻ khách hàng VIP là: \[0,9x.\left( {1 - 5\% } \right) = 0,855x\] (đồng)
Vì giá tiền của chiếc ti vi sau khi được giảm giá là \[17\,100\,000\]đồng nên ta có phương trình:
\[\begin{array}{l}0,855x = 17\,100\,000\\\,\,\,\,\,\,\,\,\,\,\,\,x = 20\,000\,000\end{array}\]
Vậy giá ban đầu của chiếc ti vi khi chưa khuyến mãi là \[20\,000\,000\](đồng)
Lời giải
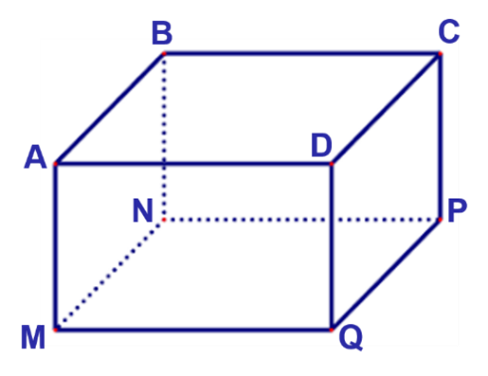
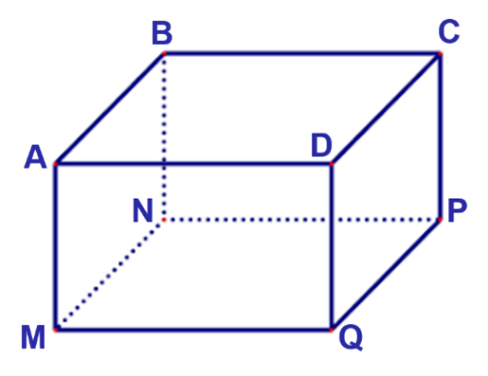
Gọi độ dài cạnh đáy \[MN\] và độ dài chiều cao \[AM\] của hộp quà lần lượt là \[x\left( {dm} \right)\], \[y\left( {dm} \right)\](\[x > 0\], \[y > 0\])
Do thể tích hộp quà là \[4d{m^3}\] nên \[{x^2}y = 4\] hay \[y = \frac{4}{{{x^2}}}\].
Tổng diện tích các mặt được mạ kim loại quý là: \[S = 4xy + {x^2} = {x^2} + \frac{{16}}{x}\]
\[S = {x^2} - 4x + 4 + \frac{{4{x^2} + 16}}{x} - 4 = {\left( {x - 2} \right)^2} + \frac{{4{{\left( {x - 2} \right)}^2}}}{x} + 12 \ge 12\]
Chứng minh được \[S \ge 12\] và dấu bằng xảy ra khi \[x = 2,y = 1\].
Vậy, để tổng diện tích các mặt được mạ kim loại quý của chiếc hộp là nhỏ nhất thì độ dài cạnh mặt đáy và chiều cao chiếc hộp lần lượt là \[2dm\] và \[1dm\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.