(0,5đ) .Bác Minh muốn đặt đóng một chiếc hộp đựng quà lưu niệm có dạng hình hộp chữ nhật với mặt đáy \[ABCD\] là hình vuông như hình dưới đây.
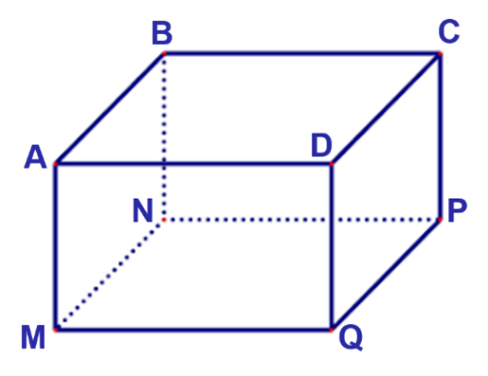
Để món quà trở nên đặc biệt, bác Minh muốn mạ bốn mặt xung quanh và mặt đáy dưới (đáy \[MNPQ\]) của chiếc hộp bằng kim loại quý (không mạ nắp hộp). Em hãy tìm độ dài cạnh \[MN\] của mặt đáy và chiều cao \[AM\] của hộp quà sao cho tổng diện tích các mặt được mạ kim loại quý của chiếc hộp là nhỏ nhất biết rằng thể tích của chiếc hộp là \[4d{m^3}\].
Để món quà trở nên đặc biệt, bác Minh muốn mạ bốn mặt xung quanh và mặt đáy dưới (đáy \[MNPQ\]) của chiếc hộp bằng kim loại quý (không mạ nắp hộp). Em hãy tìm độ dài cạnh \[MN\] của mặt đáy và chiều cao \[AM\] của hộp quà sao cho tổng diện tích các mặt được mạ kim loại quý của chiếc hộp là nhỏ nhất biết rằng thể tích của chiếc hộp là \[4d{m^3}\].
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 24 !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
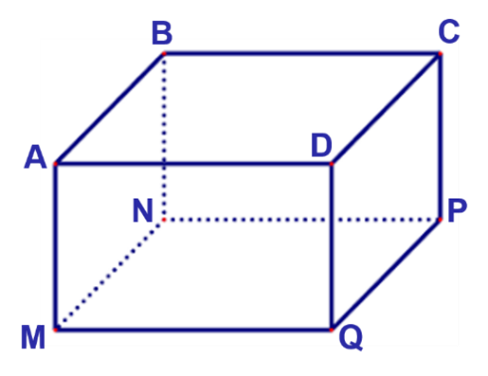
Gọi độ dài cạnh đáy \[MN\] và độ dài chiều cao \[AM\] của hộp quà lần lượt là \[x\left( {dm} \right)\], \[y\left( {dm} \right)\](\[x > 0\], \[y > 0\])
Do thể tích hộp quà là \[4d{m^3}\] nên \[{x^2}y = 4\] hay \[y = \frac{4}{{{x^2}}}\].
Tổng diện tích các mặt được mạ kim loại quý là: \[S = 4xy + {x^2} = {x^2} + \frac{{16}}{x}\]
\[S = {x^2} - 4x + 4 + \frac{{4{x^2} + 16}}{x} - 4 = {\left( {x - 2} \right)^2} + \frac{{4{{\left( {x - 2} \right)}^2}}}{x} + 12 \ge 12\]
Chứng minh được \[S \ge 12\] và dấu bằng xảy ra khi \[x = 2,y = 1\].
Vậy, để tổng diện tích các mặt được mạ kim loại quý của chiếc hộp là nhỏ nhất thì độ dài cạnh mặt đáy và chiều cao chiếc hộp lần lượt là \[2dm\] và \[1dm\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi \(x\)(đồng) là giá tiền ban đầu của chiếc ti vi khi chưa khuyến mãi \(\left( {x > 0} \right)\)
Giá tiền của chiếc ti vi sau khi được giảm giá \[10\% \] là: \[x.\left( {1 - 10\% } \right) = 0,9x\](đồng)
Giá tiền của chiếc ti vi sau khi được giảm giá thêm \[5\% \] giá đã giảm do có thẻ khách hàng VIP là: \[0,9x.\left( {1 - 5\% } \right) = 0,855x\] (đồng)
Vì giá tiền của chiếc ti vi sau khi được giảm giá là \[17\,100\,000\]đồng nên ta có phương trình:
\[\begin{array}{l}0,855x = 17\,100\,000\\\,\,\,\,\,\,\,\,\,\,\,\,x = 20\,000\,000\end{array}\]
Vậy giá ban đầu của chiếc ti vi khi chưa khuyến mãi là \[20\,000\,000\](đồng)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Diện tích Inox cần làm ra cái Téc nước hình trụ (có nắp) gồm diện tích hai đáy (đáy Téc và nắp Téc) và diện tích xung quanh của Téc nước hình trụ
Diện tích hai đáy là \({S_1} = 2\pi {R^2} = \pi {.60^2} = 7200\pi \) (cm2)
Diện tích xung quanh là \({S_2} = 2\pi Rh = 2\pi .60.220 = 26400\pi \) (cm2)
Diện tích Inox cần làm ra cái Téc nước là \(S = 7200\pi + 26400\pi = 33600\pi \)(cm2)
Hay \(S = 3,36\pi \approx 10,56\) (m2)
Vậy diện tích Inox cần làm ra cái Téc nước là \(10,56\)m2.
b) Thể tích của Téc nước hình trụ là \(V = \pi {R^2}h = \pi {.60^2}.220 = 792000\pi \) (cm3)
Hay \(V = 792\pi \approx 2488,14\) (lít)
Vậy khi Téc nước hình trụ chứa đầy nước thì được \(2488,14\) lít.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập