(4,0 điểm)
Một Téc nước hình trụ tròn có bán kính \(60\)cm, chiều cao \(220\)cm. Hỏi:
a) Diện tích Inox cần làm ra cái Téc nước (có nắp) là bao nhiêu mét vuông (giả sử phần nắp cong không đáng kể)
b) Khi Téc nước hình trụ chứa đầy nước thì được bao nhiêu lít?
a) Diện tích Inox cần làm ra cái Téc nước (có nắp) là bao nhiêu mét vuông (giả sử phần nắp cong không đáng kể)
b) Khi Téc nước hình trụ chứa đầy nước thì được bao nhiêu lít?
Câu hỏi trong đề: Đề luyện thi Toán vào lớp 10 Hà Nội 2026 có đáp án - Đề 24 !!
Quảng cáo
Trả lời:
a) Diện tích Inox cần làm ra cái Téc nước hình trụ (có nắp) gồm diện tích hai đáy (đáy Téc và nắp Téc) và diện tích xung quanh của Téc nước hình trụ
Diện tích hai đáy là \({S_1} = 2\pi {R^2} = \pi {.60^2} = 7200\pi \) (cm2)
Diện tích xung quanh là \({S_2} = 2\pi Rh = 2\pi .60.220 = 26400\pi \) (cm2)
Diện tích Inox cần làm ra cái Téc nước là \(S = 7200\pi + 26400\pi = 33600\pi \)(cm2)
Hay \(S = 3,36\pi \approx 10,56\) (m2)
Vậy diện tích Inox cần làm ra cái Téc nước là \(10,56\)m2.
b) Thể tích của Téc nước hình trụ là \(V = \pi {R^2}h = \pi {.60^2}.220 = 792000\pi \) (cm3)
Hay \(V = 792\pi \approx 2488,14\) (lít)
Vậy khi Téc nước hình trụ chứa đầy nước thì được \(2488,14\) lít.
Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn \(\left( O \right)\) đường kính \(AB = 2R\). Đường thẳng \(d\) vuông góc với bán kính \[OB\] tại \(H.\) Trên nửa đường tròn \(\left( O \right)\) lấy điểm \(M\)thay đổi (\(M \ne A,\,M \ne \,B,\,M\) không nằm trên \(d\). Tia \(AM\) cắt đường thẳng \(d\) tại \(C\). Tia \(BM\) cắt đường thẳng \(d\) tại \(D\). Tiếp tuyến tại \(M\) của đường tròn cắt đường thẳng \(d\) ở \(K\).
a) Chứng minh bốn điểm \[A,M,D,H\]cùng thuộc một đường tròn.
b) Đường thẳng \(AD\) cắt đường tròn \(\left( O \right)\) tại \(E\). Chứng minh \(B,\,E,\,C\) thẳng hàng.
c) Chứng minh \(KM = KE\).
d) Chứng minh \(ME\) luôn đi qua một điểm cố định khi \(M\)thay đổi trên đường tròn \(\left( O \right)\).
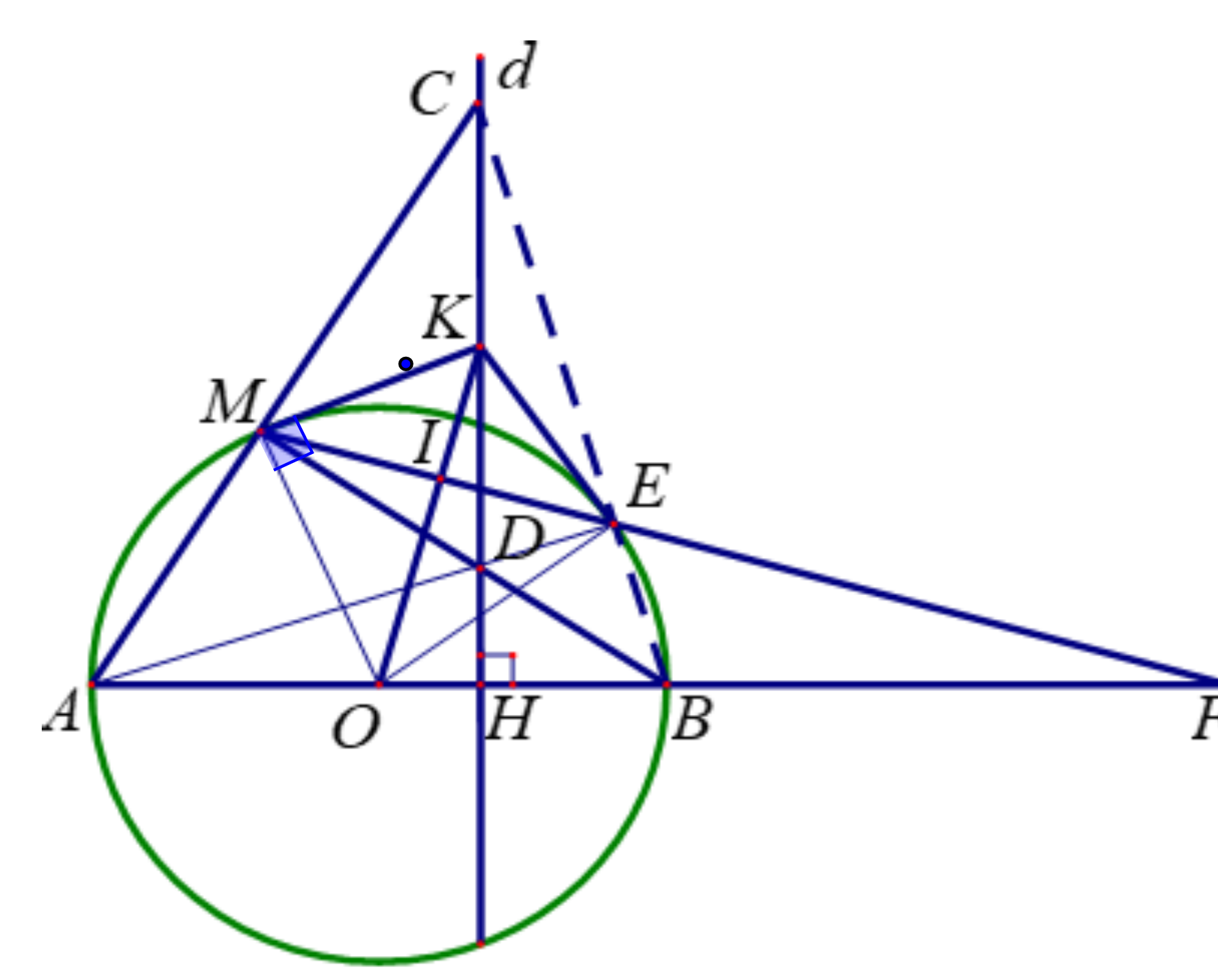
Cho đường tròn \(\left( O \right)\) đường kính \(AB = 2R\). Đường thẳng \(d\) vuông góc với bán kính \[OB\] tại \(H.\) Trên nửa đường tròn \(\left( O \right)\) lấy điểm \(M\)thay đổi (\(M \ne A,\,M \ne \,B,\,M\) không nằm trên \(d\). Tia \(AM\) cắt đường thẳng \(d\) tại \(C\). Tia \(BM\) cắt đường thẳng \(d\) tại \(D\). Tiếp tuyến tại \(M\) của đường tròn cắt đường thẳng \(d\) ở \(K\).
a) Chứng minh bốn điểm \[A,M,D,H\]cùng thuộc một đường tròn.
b) Đường thẳng \(AD\) cắt đường tròn \(\left( O \right)\) tại \(E\). Chứng minh \(B,\,E,\,C\) thẳng hàng.
c) Chứng minh \(KM = KE\).
d) Chứng minh \(ME\) luôn đi qua một điểm cố định khi \(M\)thay đổi trên đường tròn \(\left( O \right)\).

a) Có \(M\) thuộc đường tròn \(\left( O \right)\) đường kính \(AB\) nên \(\Delta AMB\) vuông tại \(M\).
Vì \(D \in MB \Rightarrow \Delta AMD\)vuông tại \(M \Rightarrow \Delta AMD\)nội tiếp đường tròn đường kính\(AD\).
\( \Rightarrow A,M,D\)tuộc đường tròn đường kính\(AD(1)\)
\(d \bot AB\) tại \(H\) nên \(\Delta AHD\) vuông tại \(H\)\( \Rightarrow \Delta AHD\)nội tiếp đường tròn đường kính\(AD\)\( \Rightarrow A,M,D\)tuộc đường tròn đường kính\(AD(2)\)
Từ \((1);(2)\) bốn điểm \[A,M,D,H\]cùng thuộc một đường tròn đường kính \(AD\)(đpcm).
b) Xét \(\Delta ABC\) có hai đường cao \(CH,\,BM\) cắt nhau tại \(D\) nên \(D\) là trực tâm
Suy ra \(AD \bot BC\,\,(3)\)
Có \(E\) thuộc đường tròn đường kính \(AB\)\( \Rightarrow \widehat {AEB} = 90^\circ \Rightarrow AE \bot BE.\, Hay\,AD \bot BE\,\,(4)\)
Từ (3) và (4) suy ra \(B,\,E,\,C\) thẳng hàng.
c) Xét \(\left( O \right)\)có \(MK\)là tiếp tuyến tại M nên \(\widehat {OMK} = {90^0} \Rightarrow \widehat {KMD} + \widehat {BMO} = {90^0}(5)\)
\(\Delta OMB\)cân tại \(O \Rightarrow \widehat {OMB} = \widehat {OBM}\),\(\widehat {KDM} = \widehat {BDH}\)(đđ),\(\widehat {HDB} + \widehat {MBO} = {90^0}(6)\)
Từ (5) và (6) suy ra \(\widehat {KMD} = \widehat {KDM} \Rightarrow \Delta KMD\)cân tại \(K \Rightarrow KM = KD\) (t/c) (7)
Có \(\widehat {DMK} + \widehat {KMC} = {90^0},\widehat {MDK} + \widehat {KCM} = {90^0},\widehat {KMD} = \widehat {KDM} \Rightarrow \widehat {KMC} = \widehat {KCM}\)
\( \Rightarrow \Delta KMC\)cân tại \(K \Rightarrow KM = KC\)(t/c) (8)
Từ (7) và (8) suy ra \(KD = KC\)
Có \(E\) thuộc đường tròn \(\left( O \right)\) đường kính \(AB\) nên \(\Delta AEB\) vuông tại \(E\).
Hay \(\Delta CED\) vuông tại \(E\)mà \(EK\)là trung tuyến nên \(EK = KD = KC = \frac{{CD}}{2}(t/c)(9)\)
Từ (8) và (9) suy ra \(KM = KE\)(đpcm)
d) Gọi \(I\) là giao điểm của \(BM\) và \(KO\), \(F\) là giao điểm của \(AB\) và \(ME\).
Có \(KM = KE,OM = OE \Rightarrow KO\) là đường trung trực của \(ME \Rightarrow KO \bot ME\) tại \(I\)
Xét \(\Delta OEK\) có \(\widehat {OEK} = 90^\circ ,\,EI \bot OK \Rightarrow OI.OK = O{E^2} = {R^2}\)
Xét \(\Delta FIO\) và \(\Delta KHO\) có: O10-2024-GV163.\(\widehat {OIF} = \widehat {OHK} = 90^\circ ,\widehat O\) chung
\[ \Rightarrow \frac{{FO}}{{KO}} = \frac{{OI}}{{OH}} \Rightarrow FO = \frac{{KO.OI}}{{OH}} = \frac{{{R^2}}}{{OH}}\] không đổi (Vì \(O,\,H\) cố định)
Suy ra điểm \(F\) nằm trên tia \(AB\) cố định và cách điểm \(H\) cố định một khoảng \[FO = \frac{{{R^2}}}{{OH}}\] không đổi nên \(F\) là điểm cố định.
Vậy \(ME\) luôn đi qua một điểm \(F\) cố định khi \(M\)thay đổi trên đường tròn \(\left( O \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\)(đồng) là giá tiền ban đầu của chiếc ti vi khi chưa khuyến mãi \(\left( {x > 0} \right)\)
Giá tiền của chiếc ti vi sau khi được giảm giá \[10\% \] là: \[x.\left( {1 - 10\% } \right) = 0,9x\](đồng)
Giá tiền của chiếc ti vi sau khi được giảm giá thêm \[5\% \] giá đã giảm do có thẻ khách hàng VIP là: \[0,9x.\left( {1 - 5\% } \right) = 0,855x\] (đồng)
Vì giá tiền của chiếc ti vi sau khi được giảm giá là \[17\,100\,000\]đồng nên ta có phương trình:
\[\begin{array}{l}0,855x = 17\,100\,000\\\,\,\,\,\,\,\,\,\,\,\,\,x = 20\,000\,000\end{array}\]
Vậy giá ban đầu của chiếc ti vi khi chưa khuyến mãi là \[20\,000\,000\](đồng)
Lời giải
Gọi độ dài cạnh đáy \[MN\] và độ dài chiều cao \[AM\] của hộp quà lần lượt là \[x\left( {dm} \right)\], \[y\left( {dm} \right)\](\[x > 0\], \[y > 0\])
Do thể tích hộp quà là \[4d{m^3}\] nên \[{x^2}y = 4\] hay \[y = \frac{4}{{{x^2}}}\].
Tổng diện tích các mặt được mạ kim loại quý là: \[S = 4xy + {x^2} = {x^2} + \frac{{16}}{x}\]
\[S = {x^2} - 4x + 4 + \frac{{4{x^2} + 16}}{x} - 4 = {\left( {x - 2} \right)^2} + \frac{{4{{\left( {x - 2} \right)}^2}}}{x} + 12 \ge 12\]
Chứng minh được \[S \ge 12\] và dấu bằng xảy ra khi \[x = 2,y = 1\].
Vậy, để tổng diện tích các mặt được mạ kim loại quý của chiếc hộp là nhỏ nhất thì độ dài cạnh mặt đáy và chiều cao chiếc hộp lần lượt là \[2dm\] và \[1dm\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.