(4,0 điểm)
Một hộp đựng bóng tenis có dạng hình trụ. Biết rằng hộp chứa vừa khít ba quả bóng tenis được xếp theo chiều dọc, các quả bóng tenis có đường kính là \(6,2{\rm{ }}cm\) và có kích thức như nhau.
a) Tính thể tích hộp đựng bóng tenis
b) Tính thể tích phần không gian còn trống bên trong là bao nhiêu? (Bỏ qua độ dày của vỏ hộp) (Lấy \(\pi \approx 3,14\) và kết quả làm tròn đến chữ số thập phân thứ nhất).
Một hộp đựng bóng tenis có dạng hình trụ. Biết rằng hộp chứa vừa khít ba quả bóng tenis được xếp theo chiều dọc, các quả bóng tenis có đường kính là \(6,2{\rm{ }}cm\) và có kích thức như nhau.
a) Tính thể tích hộp đựng bóng tenis
b) Tính thể tích phần không gian còn trống bên trong là bao nhiêu? (Bỏ qua độ dày của vỏ hộp) (Lấy \(\pi \approx 3,14\) và kết quả làm tròn đến chữ số thập phân thứ nhất).Quảng cáo
Trả lời:
a) Chiều cao của hộp hình trụ: \(3.6,2 = 18,6{\rm{ }}\left( {cm} \right)\)
Bán kính của hình tròn đáy hình trụ: \(6,2:2 = 3,1{\rm{ }}\left( {cm} \right)\)
Thể tích của hộp hình trụ là: \(V = \pi {R^2}h \approx {3,14.3,1^2}.18,6\)\( \approx 561,3{\rm{ }}\left( {c{m^3}} \right)\)
b) Thể tích của 3 quả bóng tenis là: \(V = 3.\frac{4}{3}\pi {R^3}\)\( \approx 3.\frac{4}{3}{.3,14.3,1^3}\)\( \approx 93,5{\rm{ }}\left( {c{m^3}} \right)\)
Thể tích phần không gian còn trống bên trong là: \(561,3 - 93,5 = 467,8{\rm{ }}\left( {c{m^3}} \right)\)
Câu hỏi cùng đoạn
Câu 2:
Cho đường tròn \(\left( O \right)\) và dây cung \(AB\). Trên tia đối của tia \(AB\)lấy điểm C . Từ điểm chính giữa \(P\) của cung lớn \(AB\) kẻ đường kính \(PQ\) của đường tròn (O) cắt dây \(AB\) tại \(D\). Tia \(CP\) cắt đường tròn \(\left( O \right)\) tại điểm \(I\)( điểm \(I\) khác điểm \(P\)). Các dây \(AB\) và \(QI\) cắt nhau tại \(K\)
a) Chứng minh tứ giác \(PDKI\) nội tiếp
b) Chứng minh rằng \(CI.CP = CK.CD\) và \(IC\) là phân giác góc ngoài tại đỉnh \(I\) của tam giác \(AIB\) .
c) Giả sử ba điểm\(A;B;C\) cố định. Chứng minh khi đường tròn \(\left( O \right)\) thay đổi nhưng vẫn đi qua hai điểm\(A\) và \(B\) thì đường thẳng \(QI\) luôn đi qua một điểm cố định.
Cho đường tròn \(\left( O \right)\) và dây cung \(AB\). Trên tia đối của tia \(AB\)lấy điểm C . Từ điểm chính giữa \(P\) của cung lớn \(AB\) kẻ đường kính \(PQ\) của đường tròn (O) cắt dây \(AB\) tại \(D\). Tia \(CP\) cắt đường tròn \(\left( O \right)\) tại điểm \(I\)( điểm \(I\) khác điểm \(P\)). Các dây \(AB\) và \(QI\) cắt nhau tại \(K\)
a) Chứng minh tứ giác \(PDKI\) nội tiếp
b) Chứng minh rằng \(CI.CP = CK.CD\) và \(IC\) là phân giác góc ngoài tại đỉnh \(I\) của tam giác \(AIB\) .
c) Giả sử ba điểm\(A;B;C\) cố định. Chứng minh khi đường tròn \(\left( O \right)\) thay đổi nhưng vẫn đi qua hai điểm\(A\) và \(B\) thì đường thẳng \(QI\) luôn đi qua một điểm cố định.

a) Chứng minh: Tứ giác \(PDKI\) nội tiếp
Ta có \(PQ\) là đường kính của đường tròn (O). Suy ra \(\widehat {PIQ} = 90^\circ \) suy ra \[CI.CP = CD.CK\]
Do P là điểm chính giữa của cung lớn AB. Suy ra PA = PB
Mà OA = OB (cùng là bán kính của (O))
Suy ra PO là đường trung trực của AB suy ra \(OP \bot AB\) tại D
Suy ra \(PQ \bot AB\)
\(\widehat {PDK} = 90^\circ \)
Nên \(\widehat {PDK} + \widehat {PIK} = 90^\circ + 90^\circ = 180^\circ \)
Tứ giác \({\rm{PDKI }}\)nội tiếp (hai góc đối bù nhau )
b) Xét tam giác \(CIK\) và tam giác \(CDP\) ta có :
\[\widehat C\] chung
\[\widehat {CIK} = \widehat {CDP} = 90^\circ \]
\[\frac{{CI}}{{CD}} = \frac{{CK}}{{CP}}\] suy ra \[CI.CP = CD.CK\]
\[CI.CP = CD.CK\]
Ta có PO là đường trung trực của AB, hay PQ là đường trung trực của AB
\({\rm{QA}}\,{\rm{ = }}\,{\rm{QB}}\) hay điểm \(Q\) là điểm chính giữa cung nhỏ nên
Do đó \(\widehat {AIQ} = \widehat {BIQ}\) ( hai góc nội tiếp chắn hai cung bằng nhau thì bằng nhau )
Hay \(IK\) là đường phân giác trong của tam giác \(AIB\) ; và lại có \(IK \bot IC{\rm{ ( }}\widehat {PIQ} = 90^\circ )\)
nên \(IC\) là đường phân giác góc ngoài tại đỉnh \(I\) của tam giác \(AIB\)
c) Ta đi chứng minh \(K\) là điểm cố định
Ta có điểm \(D\) là trung điểm \(AB({\rm{ OD}} \bot {\rm{AB)}}\)
Do \(ABPI\) là tứ giác nội tiếp
\(\widehat {CAI} = \widehat {CPB}\)
\(\frac{{CA}}{{CP}} = \frac{{CI}}{{CB}}\)
\(CA.CB = CI.CP\)
Vậy nên \(CA.CB = CK.CD\left( { = CI.CP} \right)\)
\(CK.CD = \left( {CD - DA} \right)\left( {CD + DB} \right)\)
\(CK.CD = \left( {CD - \frac{{AB}}{2}} \right)\left( {CD + \frac{{AB}}{2}} \right)\)
\(CK.CD = C{D^2} - \frac{{A{B^2}}}{4}\)
\(C{D^2} - CK.CD = \frac{{A{B^2}}}{4}\)
\(CD.KD = \frac{{A{B^2}}}{4}\)
\(KD = \frac{{A{B^2}}}{{4CD}}\)
Vì\(A;{\rm{ }}B;{\rm{ }}C;{\rm{ }}D\) là bốn điểm cố định nên \(K\) điểm cố địnhHot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi số áo tổ một may được trong một ngày là \[x\] (áo), (\(x \in {\mathbb{N}^*};\;x > 10\)).
Gọi số áo tổ hai may được trong một ngày là \[y\] (áo), (\(y \in {\mathbb{N}^*}\)).
Vì tổ thứ nhất may trong \[3\] ngày, tổ thứ hai may trong \[5\] ngày thì cả hai tổ may được \[1310\] chiếc áo nên ta có phương trình : \(3x + 5y = 1310\) (1).
Vì trong mỗi ngày tổ thứ nhất may được nhiều hơn tổ thứ hai \[10\] chiếc áo nên ta có phương trình: \(x - y = 10\) hay \(x = y + 10\).
Thay \(x = y + 10\) vào phương trình (1) ta được:
\(3\left( {y + 10} \right) + 5y = 1310\)
\(3y + 30 + 5y = 1310\)
\(8y = 1280\)
\(y = 160\) (tm).
Suy ra \(x = 160 + 10 = 170\) (tm).
Mỗi ngày tổ một may được \(170\) áo, tổ hai may được \(160\) áo.
Lời giải
a)
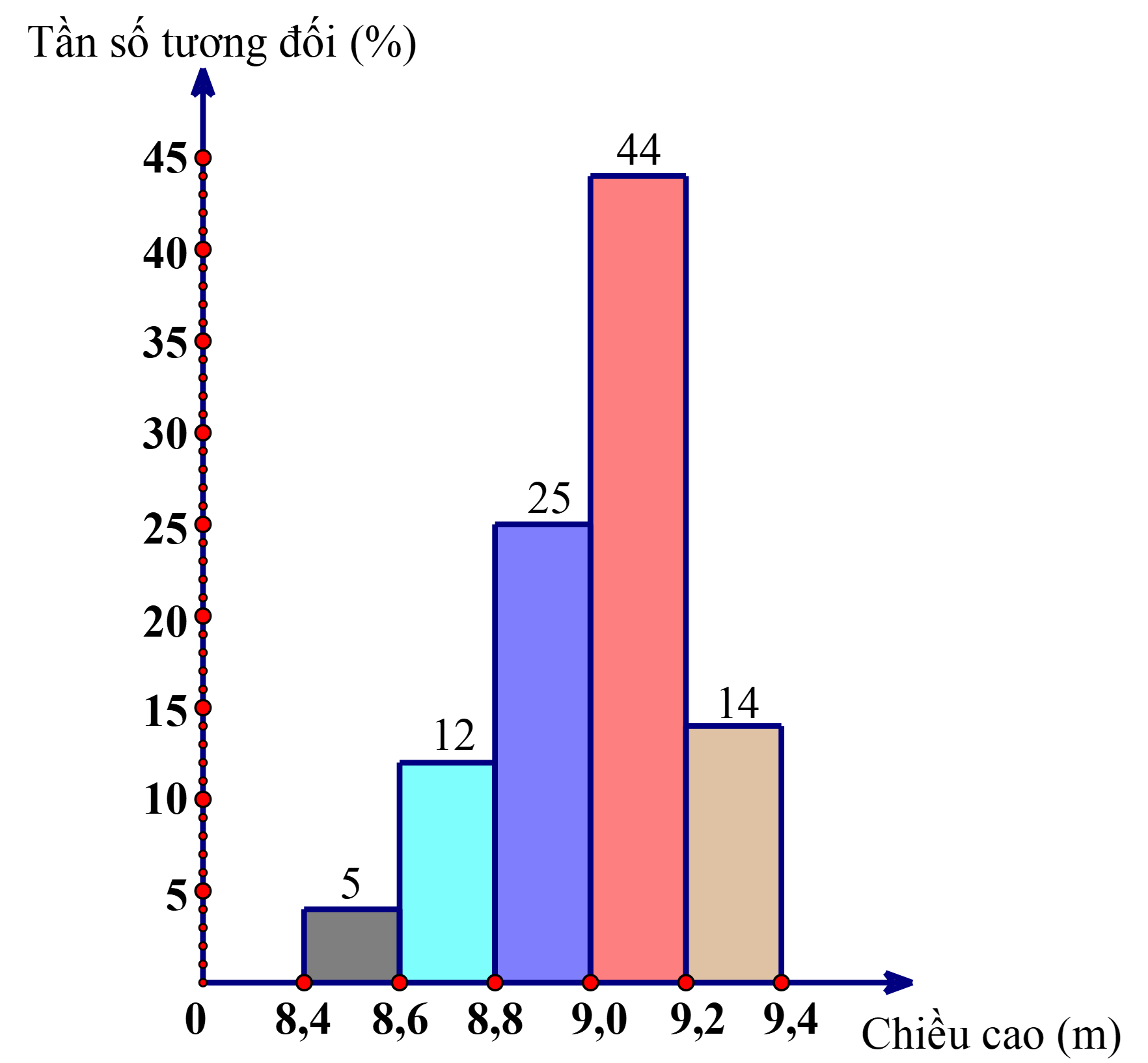
Tần số tương đối ghép nhóm của nhóm \(\left[ {8,4;8,6} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{5.100}}{{100}}\% = 5\% ;.\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {8,6;8,8} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{12.100}}{{100}}\% = 12\% ;\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {8,8;9,0} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{25.100}}{{100}}\% = 25\% ;\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {9,0;9,2} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{44.100}}{{100}}\% = 44\% ;\)
Tần số tương đối ghép nhóm của nhóm \(\left[ {9,2;9,4} \right)\) là: \(f = \frac{n}{N}.100\% = \frac{{14.100}}{{100}}\% = 14\% ;\)
Vì vậy, bảng tần ghép nhóm của mẫu số liệu đã cho được nêu trong bảng dưới đây.
|
Chiều cao (\[m\]) |
\(\left[ {8,4;8,6} \right)\) |
\(\left[ {8,6;8,8} \right)\) |
\(\left[ {8,8;9,0} \right)\) |
|
\(\left[ {9,0;9,2} \right)\) |
\(\left[ {9,2;9,4} \right)\) |
Tổng |
|
Tần số tương đối (\(\% \)) |
\(5\) |
\(12\) |
\(25\) |
|
\(44\) |
\(14\) |
\(100\) |
b) Biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng
thống kê thu được ở câu a
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.