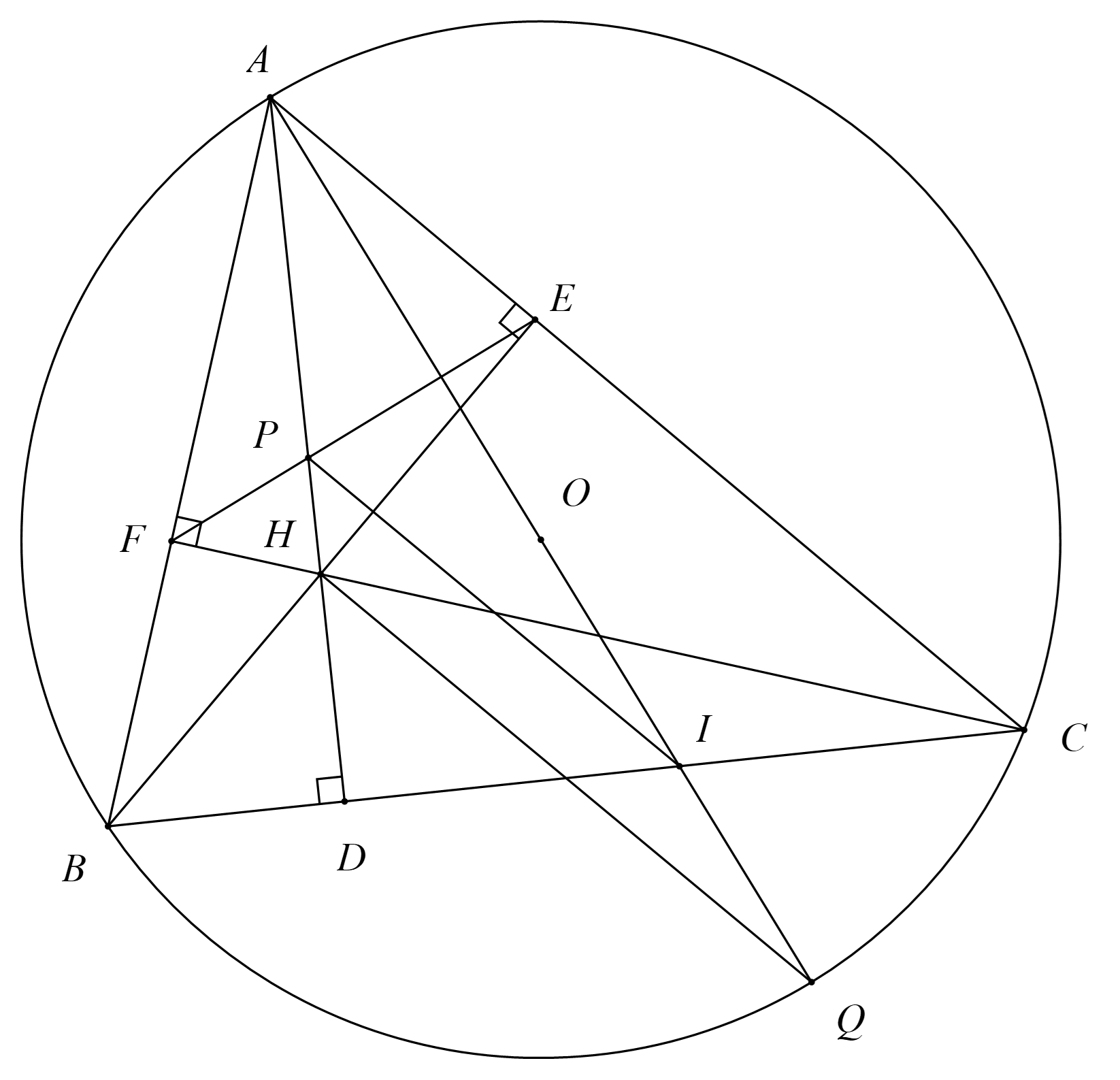
Cho tam giác \[{\rm{ABC}}\] nhọn nội tiếp đường trong \[{\rm{(O)}}\], các đường cao \[{\rm{AD}}{\rm{, BE}}{\rm{,CF}}\] cắt nhau tại \[{\rm{H}}{\rm{.}}\]Kẻ đường kính \[{\rm{AQ}}\] của đường tròn \[{\rm{(O)}}\]cắt cạnh \[{\rm{BC}}\] tại \[{\rm{I}}{\rm{.}}\]

1)   Chứng minh bốn điểm \[A,F,H,E\]cùng thuộc một đường tròn.

2)   Gọi \[{\rm{P}}\]là giao điểm của \[{\rm{AH}}\] và \[EF\]. Chứng minh \(\widehat {BAD}\) = \(\widehat {CAQ}\)

3) Chứng minh rằng: \[\Delta AEP\]∽\[\Delta ABI\]và \[PI\parallel HQ\]

Gọi dân số nội thành và ngoại thành lần lượt là \[{\rm{a}}{\rm{,}}\;{\rm{b}}\](\[0 < a,b < 420\], nghìn người)

Ta có: dân số của một tỉnh hay tổng của \[{\rm{a}}\] và \[{\rm{b}}\]là \[{\rm{420}}\] nghìn người nên \[a + b = 420\]

Dân số nội thành là: \[100,8\% a{\rm{ }} = {\rm{ }}1,008a\](người)

Dân số ngoại thành là: \[101,1\% b{\rm{ }} = {\rm{ }}1,011b\](người)

Vì sau một năm dân số toàn tỉnh sẽ tăng 1% nên ta có pt:

\[1,008a\; + {\rm{ }}1,011b\; = {\rm{ }}420{\rm{ }}.101\% \]

\[1,008a\; + {\rm{ }}1,011b\; = {\rm{ }}424,2\]

Ta có hệ phương trình: \[\left\{ \begin{array}{l}a + b = 420\\1,008a\; + {\rm{ }}1,011b\; = {\rm{ }}424,2\end{array} \right.\]

Giải hệ phương trình ta được: \[a = 140;{\rm{ }}b = 280\] 

Vậy dân số nội thành là \[{\rm{140}}\] nghìn người, dân số ngoại thành là \[{\rm{280}}\] nghìn người.

Với \(x,y,z \ge 0\)

Ta đi chứng minh: \({x^3} + {y^3} + {z^3} \ge 3xyz\)

\({x^3} + 3{x^2}y + 3x{y^2} + {y^3} - 3{x^2}y - 3x{y^2} + {z^3} - 3xyz \ge 0\)

\({\left( {x + y} \right)^3} - 3xy\left( {x + y} \right) + {z^3} - 3xyz \ge 0\)

\({\left( {x + y} \right)^3} + {z^3} - 3xy\left( {x + y} \right) - 3xyz \ge 0\)

\(\left( {x + y + z} \right)\left[ {{{\left( {x + y} \right)}^2} - \left( {x + y} \right)z + {z^2}} \right] - 3xy\left( {x + y + z} \right) \ge 0\)

\(\left( {x + y + z} \right)\left[ {{x^2} + 2xy + {y^2} - xz - yz + {z^2}} \right] - 3xy\left( {x + y + z} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {{x^2} + 2xy + {y^2} - xz - yz + {z^2} - 3xy} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {{x^2} + {y^2} + {z^2} - xy - xz - yz} \right) \ge 0\)

\(2\left( {x + y + z} \right)\left( {{x^2} + {y^2} + {z^2} - xy - xz - yz} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {2{x^2} + 2{y^2} + 2{z^2} - 2xy - 2xz - 2yz} \right) \ge 0\)

\(\left( {x + y + z} \right)\left( {{x^2} - 2xy + {y^2} + {x^2} - 2xz + {z^2} + {y^2} - 2yz + {z^2}} \right) \ge 0\)

\(\left( {x + y + z} \right)\left[ {{{\left( {x - y} \right)}^2} + {{\left( {x - z} \right)}^2} + {{\left( {y - z} \right)}^2}} \right] \ge 0\) (Luôn đúng với mọi \(x,y,z \ge 0\))

Vậy nên \({x^3} + {y^3} + {z^3} \ge 3xyz\)

 Gọi cạnh hình vuông nhỏ là \(x(m,0 < x < 1)\)

Chiều cao của hình hộp là \(x\) (m) 

Chiều dài, chiều rộng của hộp hình hộp là \(1 - 2x\) (m)

Thể tích của hộp hình lập phương khi đó là:  \(({m^3})\)

\(x.(1 - 2x)(1 - 2x)\)\( = \frac{1}{4}.4x.(1 - 2x)(1 - 2x)\)

Áp dụng bất đẳng thức Cauchy ta có:

\(4x.(1 - 2x)(1 - 2x) \le {\left( {\frac{{4x + 1 - 2x + 1 - 2x}}{3}} \right)^3}\)

\(\frac{1}{4}.4x.(1 - 2x)(1 - 2x) \le \frac{1}{4}{\left( {\frac{{4x + 1 - 2x + 1 - 2x}}{3}} \right)^3}\)

\(\frac{1}{4}.4x.(1 - 2x)(1 - 2x) \le \frac{1}{4}.{\left( {\frac{2}{3}} \right)^3} = \frac{2}{{27}}\)

Dấu bằng xảy ra khi \[4x = 1 - 2x\]

\[6x = 1\]

\(x = \frac{1}{6}(TM)\)