Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều rộng của hầm là 12 m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8 m thì có chiều rộng không quá 3 m. Hỏi chiếc xe tải có chiều cao 2,8 m có thể đi qua hầm được không?
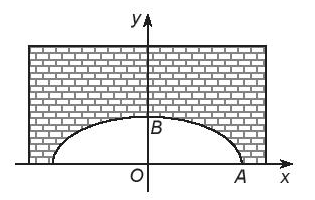
Một người kĩ sư thiết kế một đường hầm một chiều có mặt cắt là một nửa hình elip, chiều rộng của hầm là 12 m, khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m. Người kĩ sư này muốn đưa ra cảnh báo cho các loại xe có thể đi qua hầm. Biết rằng những loại xe tải có chiều cao 2,8 m thì có chiều rộng không quá 3 m. Hỏi chiếc xe tải có chiều cao 2,8 m có thể đi qua hầm được không?

Quảng cáo
Trả lời:
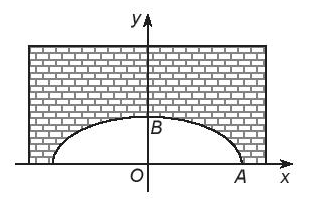
Giả sử phương trình chính tắc của elip là: \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) (trong đó \(a > b > 0\)).
Vì chiều rộng của hầm là 12 m nên \(OA = 12:2 = 6\) (m) nên điểm \(A\) có tọa độ \(\left( {6;\,\,0} \right)\).
Khoảng cách từ điểm cao nhất của elip so với mặt đường là 3 m nên \(OB = 3\) m, do đó điểm \(B\) có tọa độ \(\left( {0;\,\,3} \right)\).
Do các điểm \(B\left( {0;\,\,3} \right)\) và \(A\left( {6;\,\,0} \right)\) thuộc elip nên thay vào phương trình của elip ta được:
\(\frac{{{0^2}}}{{{a^2}}} + \frac{{{3^2}}}{{{b^2}}} = 1 \Rightarrow {b^2} = {3^2} = 9\)
\(\frac{{{6^2}}}{{{a^2}}} + \frac{{{0^2}}}{{{b^2}}} = 1 \Rightarrow {a^2} = {6^2} = 36\)
Suy ra phương trình của elip là: \(\frac{{{x^2}}}{{36}} + \frac{{{y^2}}}{9} = 1\).
Với những xe tải có chiều cao 2,8 m, chiều rộng của xe tải là 3 m, nếu xe chạy chính giữa hầm thì khoảng cách từ tâm xe tới mỗi bên xe không quá \(3:2 = 1,5\) m, tương ứng với \(x = 1,5\). Thay vào phương trình của elip để ta tìm ra độ cao \(y\) của điểm \(M\) (có hoành độ bằng 1,5 thuộc elip) so với trục \(Ox\). Ta có: \(\frac{{{x_M}^2}}{{36}} + \frac{{{y_M}^2}}{9} = 1\).
Suy ra: \({y_M} = 3.\sqrt {1 - \frac{{x_M^2}}{{36}}} = 3.\sqrt {1 - \frac{{{{1,5}^2}}}{{36}}} \approx 2,905 > 2,8\).
Kết luận: Ô tô tải có thể đi được qua hầm, tuy nhiên cần khuyến cáo ô tô phải đi vào chính giữa hầm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Từ điều kiện ta có
\({x^2} + {y^2} = \frac{{{{\left( {x + y} \right)}^2} + {{\left( {x - y} \right)}^2}}}{2} = 5 - {z^2} \Rightarrow {\left( {x + y} \right)^2} = 10 - 2{z^2} - {\left( {3 - z} \right)^2}\).
Do đó \({\left( {x + y} \right)^2} = 1 + 6z - 3{z^2}\).
Dễ thấy \(z \ne - 2\). Ta có \(P.\left( {z + 2} \right) + 2 = x + y\).
Do đó \({\left[ {P.\left( {z + 2} \right) + 2} \right]^2} = 1 + 6z - 3{z^2}\)
\( \Leftrightarrow {\left( {z + 2} \right)^2}{P^2} + 4\left( {z + 2} \right)P + 4 = 1 + 6z - 3{z^2}\)
\( \Leftrightarrow \left( {{P^2} + 3} \right){z^2} + \left( {4{P^2} + 4P - 6} \right)z + 4{P^2} + 8P + 3 = 0\)
Phương trình ẩn \(z\) có nghiệm khi và chỉ khi \({\Delta '_z} \ge 0\)
\( \Leftrightarrow {\left( {2{P^2} + 2P - 3} \right)^2} - \left( {{P^2} + 3} \right)\left( {4{P^2} + 8P + 3} \right) \ge 0\)
\( \Leftrightarrow 4{P^4} + 4{P^2} + 9 + 8{P^3} - 12{P^2} - 12P - \left( {4{P^4} + 8{P^3} + 3{P^2} + 12{P^2} + 24P + 9} \right) \ge 0\)
\( \Leftrightarrow 23{P^2} + 36P \le 0\)
\( \Leftrightarrow - \frac{{36}}{{23}} \le P \le 0\) (áp dụng định lí về dấu của tam thức bậc hai).
Ta có \(P = 0\) khi \[x = 2,{\rm{ }}y = 0,{\rm{ }}z = 1\] và \(P = - \frac{{36}}{{23}}\) khi \(x = \frac{{20}}{{31}},\,\,y = - \frac{{66}}{{31}},\,\,z = \frac{7}{{31}}\).
Vậy giá trị lớn nhất của \(P\) là 0 tại \[x = 2,{\rm{ }}y = 0,{\rm{ }}z = 1\].
Câu 2
Lời giải
Đáp án đúng là: A
Bình phương hai vế của phương trình \(\sqrt {57x + 31{x^2} + 2} = 5x + 4\) ta được:
\(57x + 31{x^2} + 2 = 25{x^2} + 40x + 16\).
Thu gọn phương trình trên ta được: \(6{x^2} + 17x - 14 = 0\).
Từ đó suy ra \(x = - \frac{7}{2}\) hoặc \(x = \frac{2}{3}\).
Lần lượt thay các giá trị này vào phương trình đã cho ta thấy chỉ có \(x = \frac{2}{3}\) thỏa mãn.
Do đó, tập nghiệm của phương trình là \(S = \left\{ {\frac{2}{3}} \right\}\). Mà \(\frac{2}{3} \notin \mathbb{Z}\). Vậy phương trình đã cho không có nghiệm nguyên.
Câu 3
A. \[{d_1}\] và \({d_2}\) song song với nhau;
B. \[{d_1}\] và \({d_2}\) trùng nhau;
C. \[{d_1}\] và \({d_2}\) cắt nhau và không vuông góc với nhau;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[S = \left( { - \infty ;\,\, - 3} \right) \cup \left( {2;\,\, + \infty } \right)\];
B. \(S = \left[ { - 2;\,\,3} \right]\);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Nếu \(\Delta > 0\) thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\);
B. Nếu \(\Delta < 0\) thì \(f\left( x \right)\) luôn trái dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\);
C. Nếu \(\Delta < 0\) thì \(f\left( x \right)\) luôn cùng dấu với hệ số \(b\) với mọi \(x \in \mathbb{R}\);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(5x - 3y - 5 = 0\);
B. \(3x + 5y - 37 = 0\);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.