Một hộp kín chứa \[3\] viên bi màu đỏ và \[7\] viên bi màu vàng, các viên bi có kích thước và khối lượng như nhau. Lấy ngẫu nhiên một viên bi từ trong hộp. Xác suất lấy được viên bi màu đỏ là

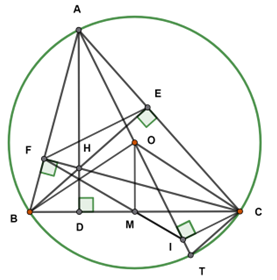
a)  Xét tứ giác \[BCEF\] ta có: \[\widehat {BFC} = \widehat {BEC} = 90^\circ \]\[(BE,CF\]là đường cao)

Suy ra tứ giác \[BCEF\]nội tiếp đường tròn đường kính \[BC\].

b) Ta có \[\widehat {ACT} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn \[(O)\]).

Xét \[\Delta ADB\] và \[\Delta ACT\] ta có:

\[\widehat {ACT} = \widehat {ADB} = 90^\circ \]

\[\widehat {ABD} = \widehat {ATC}\] (cùng chắn cung \[AC\])                   

Do đó  (g.g)                    

Ta có:  (cùng chắn cung \[AC\])

Vì tứ giác \[BCEF\] nội tiếp nên          

  \[ \Rightarrow \]

   \[ \Rightarrow \]                    

c)  Ta có \[\Delta AOC\]cân tại \[O\], \[OM\]là đường trung tuyến nên \[OM\] cũng là đường phân giác, đường cao

Do đó \[\widehat {BAC} = \widehat {MOC} = \frac{1}{2}\widehat {BOC}\]

Tương tự \[\widehat {BAC} + \widehat {ACF} = \widehat {MOC} + \widehat {OCM} = 90^\circ \]

Nên \[\widehat {ACF} = \widehat {OCM}\] (1)

Xét tứ giác \[OMIC\]ta có \[\widehat {OMC} = \widehat {OIC} = 90^\circ \]

Suy ta tứ giác \[OMIC\] nội tiếp đường tròn đường kính \[OC\]

Do đó \[\widehat {OCM} = \widehat {OIM}\] (cùng chắn cung \[OM\]) (2)

Xét tứ giác \[AFIC\] ta có\[\widehat {AFI} = \widehat {AIC} = 90^\circ \]

Suy ta tứ giác \[AFIC\] nội tiếp đường tròn đường kính \[AC\]

Do đó \[\widehat {AIF} = \widehat {ACF}\] (cùng chắn cung \[OM\]) (3)

Từ (1), (2) và (3) suy ra \[\widehat {AIF} = \widehat {OIM}\]

Do đó hai tia \[IF.\;IM\] trùng nhau.

Vậy ba điểm \[F\,,\,\,M\,,\,\,I\] thẳng hàng.

Gọi \[x\;{\rm{(km/h)}}\]là tốc độ của xa máy lúc đi (ĐK: \[x\; > 0\])

Tốc độ của xe máy lúc về: \[x\; + 10\] (km/h)                             

Thời gian của xe máy lúc đi: \[\frac{{100}}{x}\] (h)

Thời gian của xe máy lúc về: \[\frac{{100}}{{x + 10}}\](h)                              

4 giờ 30 phút = \[\frac{9}{2}\] giờ

Thời gian cả đi và về là 4 giờ 30 phút nên ta có phương trình:

\[\frac{{100}}{x} + \frac{{100}}{{x + 10}} = \frac{9}{2}\]                                                                  

\[100.2(x + 10) + 100.2x = 9x(x + 10)\]

\[200x + 2000 + 200x = 9{x^2} + 90x\]

\[9{x^2} - 310x - 2000 = 0\]

Giải phương trình ta được: \[{x_1} = 40\;(N);\;{x_2} = \frac{{ - 50}}{9}(L)\]                     

Vậy tốc độ lúc đi của xe máy là 40 km/h.