a) Trong một môn học, thầy giáo có \(20\) câu hỏi khác nhau, trong đó có \(10\) câu hỏi dễ, \(6\) câu hỏi trung bình và \(4\) câu hỏi khó. Từ \(20\)câu hỏi đó lập được bao nhiêu đề kiểm tra, mỗi đề gồm \(5\) câu hỏi, sao cho đề kiểm tra phải có đủ ba loại câu hỏi và có đúng \(2\) câu hỏi dễ.
b) Tính tổng \(T = C_4^0 + 2C_4^1 + 4C_4^2 + 8C_4^3 + 16C_4^4\).
a) Trong một môn học, thầy giáo có \(20\) câu hỏi khác nhau, trong đó có \(10\) câu hỏi dễ, \(6\) câu hỏi trung bình và \(4\) câu hỏi khó. Từ \(20\)câu hỏi đó lập được bao nhiêu đề kiểm tra, mỗi đề gồm \(5\) câu hỏi, sao cho đề kiểm tra phải có đủ ba loại câu hỏi và có đúng \(2\) câu hỏi dễ.
b) Tính tổng \(T = C_4^0 + 2C_4^1 + 4C_4^2 + 8C_4^3 + 16C_4^4\).
Quảng cáo
Trả lời:
Hướng dẫn giải
a) Để tạo đề kiểm tra gồm \(5\) câu hỏi sao cho có đủ ba loại câu hỏi và có đúng \(2\) câu hỏi dễ sẽ có các phương án sau:
- Phương án 1: Đề gồm \(2\) câu hỏi dễ, \(2\) câu trung bình và \(1\) câu khó có \(C_{10}^2.C_6^2.C_4^1 = 2700\) đề.
- Phương án 2: Đề gồm \(2\) câu hỏi dễ, \(3\) câu trung bình có \(C_{10}^2.C_6^3 = 900\) đề.
- Phương án 3: Đề gồm \(2\) câu hỏi dễ, \(1\) câu trung bình và \(2\) câu khó có \(C_{10}^2.C_6^1.C_4^2 = 1620\) đề.
Áp dụng quy tắc cộng có \(2700 + 900 + 1620 = 5220\) đề.
b) Ta có: \(T = C_4^0 + 2C_4^1 + 4C_4^2 + 8C_4^3 + 16C_4^4\)
\( = C_4^0{.1^4} + C_4^1{.1^3}.2 + C_4^2{.1.2^2} + C_4^3{.1.2^3} + C_4^4{.1.2^4}\)
\( = {\left( {1 + 2} \right)^4}\)
\( = {3^4}\)
\( = 81\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: B
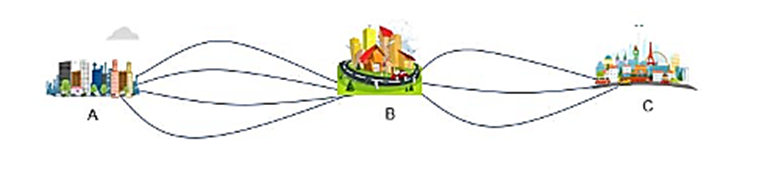
Cách để đi từ thành phố \(A\) đến thành phố \(C\) phải đi qua thành phố \(B\) gồm \(2\) giai đoạn:
- Giai đoạn 1: Đi từ thành phố \(A\) đến thành phố \(B\) có 4 cách.
- Giai đoạn 1: Ứng với mỗi cách của giai đoạn 1, từ thành phố \(B\) đến thành phố \(C\) có \(3\) cách.
Áp dụng quy tắc nhân có \(4.3 = 12\) cách để đi từ thành phố \(A\) đến thành phố \(C\).
Câu 2
Lời giải
Hướng dẫn giải
Đáp án đúng là: C
Ta có cách chia 9 người thành 3 tổ có \(C_9^3.C_6^3.C_3^3 = 1\,\,680\)
Tổ 1 có \(C_3^1\) cách chọn bác sĩ, \(C_6^2\) cách chọn người còn lại. Do đó \(C_3^1.C_6^2 = 45\) cách.
Tổ 2 có \(C_2^1\) cách chọn bác sĩ, \(C_4^2\) cách chọn người còn lại. Do đó \(C_2^1.C_4^2 = 12\) cách.
Tổ 3 có \(C_1^1\) cách chọn bác sĩ, \(C_2^2\) cách chọn người còn lại. Do đó \(C_1^1.C_2^2 = 1\) cách.
Tổng có: \(45.12.1 = 540\) cách chia thành 3 tổ để mỗi tổ đều có bác sĩ .
Do đó xác suất để mỗi tổ đều có bác sĩ là \(\frac{{540}}{{1\,\,680}} = \frac{9}{{28}}\).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.