(1,0 điểm). Một mảnh đất hình chữ nhật có chiều dài lớn hơn chiều rộng \(12\;m.\) Ở chính giữa mảnh đất người ta làm một vườn hoa hình vuông cạnh bằng \(2\;m\) (minh họa hình bên). Biết diện tích còn lại của mảnh đất (không tính phần đất làm vườn hoa) là \(104\;{m^2},\) tính chiều dài và chiều rộng của mảnh đất.
(1,0 điểm). Một mảnh đất hình chữ nhật có chiều dài lớn hơn chiều rộng \(12\;m.\) Ở chính giữa mảnh đất người ta làm một vườn hoa hình vuông cạnh bằng \(2\;m\) (minh họa hình bên). Biết diện tích còn lại của mảnh đất (không tính phần đất làm vườn hoa) là \(104\;{m^2},\) tính chiều dài và chiều rộng của mảnh đất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Gọi chiều rộng mảnh đất là \(x\,(m),\,\;x > 2\). Chú ý: Thí sinh đặt điều kiện \(x > 0\) vẫn chấm tối đa 0,25 điểm. |
|
Chiều dài mảnh đất là \(x + 12\,(m)\) và diện tích mảnh đất ban đầu là \(x(x + 12)\,({m^2})\) |
|
Vì diện tích vườn hoa bằng \(4\,{m^2}\)và diện tích còn lại của mảnh đất là \(104\;{m^2},\) nên ta có phương trình \(x(x + 12) - 4 = 104\) hay \({x^2} + 12x - 108 = 0.\) |
|
Giải phương trình được \({x_1} = - 18\) (loại), \({x_2} = 6\)(thỏa mãn). Vậy mảnh đất có chiều rộng là \(6\,m\) và chiều dài là \(18\,m.\) Chú ý: Trong bước giải phương trình, nếu chỉ đưa ra kết quả đúng vẫn chấm điểm tối đa ý đó. |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
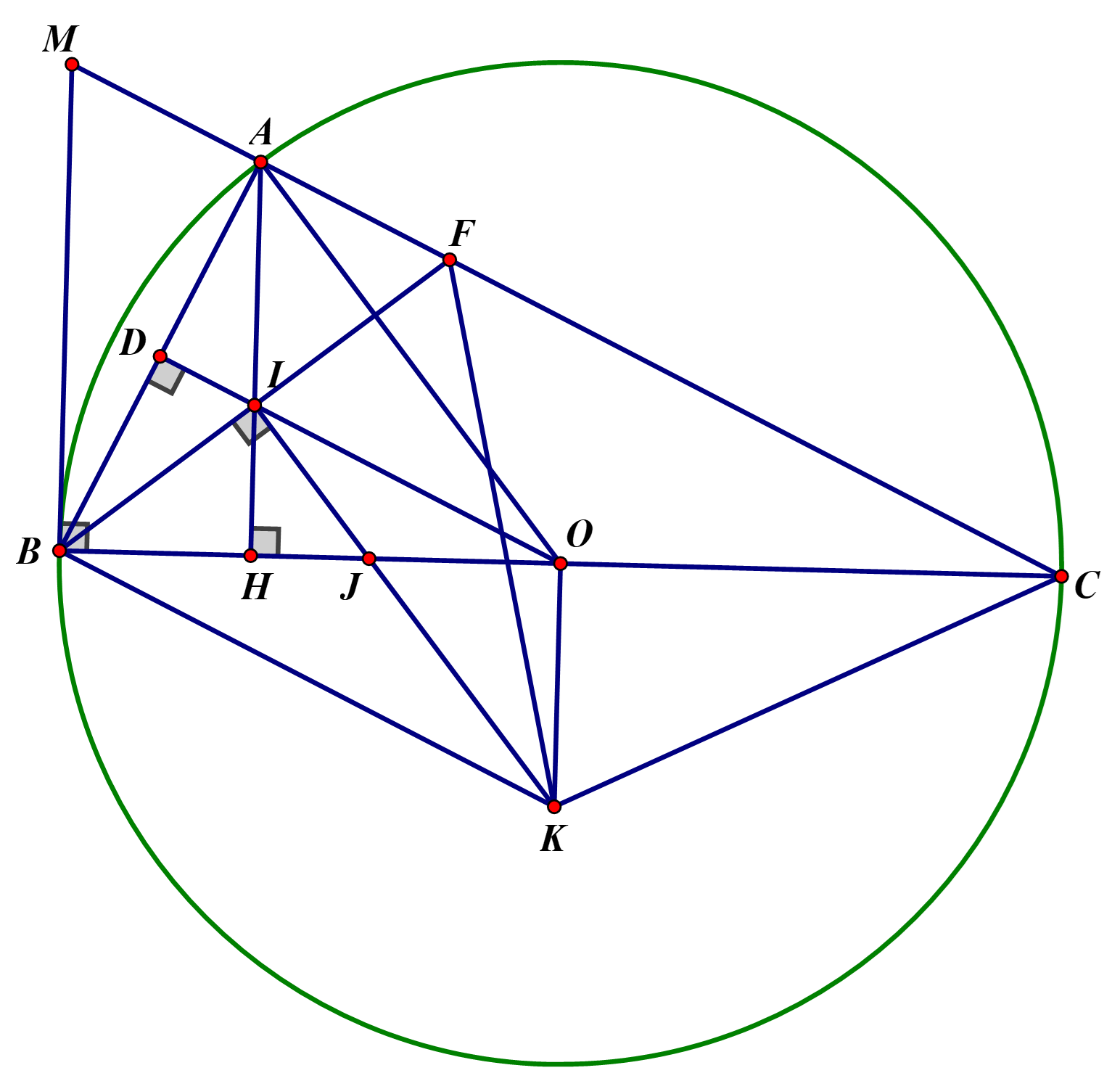
Vẽ đủ hình ý a) |
|
Chỉ ra tam giác \(ADO\) và tam giác\(AHO\)là hai tam giác vuông nội tiếp đường tròn đường kính\(AO.\) |
|
Từ đó suy ra bốn điểm \(A,\,D,\,H,\,O\) cùng thuộc đường stròn đường kính \(AO.\) |
|
b) Chứng minh hai tam giác \(ABM\) và \(HAB\) đồng dạng. |
|
Từ đó suy ra \(A{B^2} = AH.BM.\) |
|
Chỉ ra \(\Delta OAB\)cân tại \(O,\) đường cao \(OD\) nên \(OD\)là trung trực của \(AB.\) Suy ra \(IA = IB\) nên \(\widehat {IAB} = \widehat {IBA.}\) |
|
Chỉ ra \(BA\) vừa là đừng cao, vừa là phân giác của \(\Delta MBF\) nên suy ra \(AM = AF.\) |
|
c) Chỉ ra \(OD\) là phân giác \(\widehat {AOB}\) nên \(\widehat {AOD} = \widehat {BOD} = \widehat {OIK}.\) Gọi \(J\) là giao điểm của \(IK\) và \(BO.\) Chỉ ra \(\Delta BJK\)và \(\Delta IJO\) là hai tam giác cân tại \(J.\) Khi đó \(\Delta BIJ = \Delta KOJ\) (c.g.c) nên \(KO\) vuông góc \(BC\) và là trung trực của \(BC.\) |
|
Chỉ ra được \(K\)là tâm đường tròn ngoại tiếp \(\Delta BFC\). Suy ra \(KF = KC\)nên \(\Delta KFC\) là tam giác cân tại K. |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
|
Theo định lý Viète \(\left\{ \begin{array}{l}{x_1} + {x_2} = 19\\{x_1}.{x_2} = 9.\end{array} \right.\) Ta có \({\left( {\sqrt {{x_1}} + \sqrt {{x_1}} } \right)^2} = {x_1} + {x_2} + 2\sqrt {{x_1}.{x_2}} = 19 + 6 = 25\)nên \(\sqrt {{x_1}} + \sqrt {{x_2}} = 5.\) |
|
\(a + b = \sqrt {{x_1}} + 3\sqrt {{x_2}} + \sqrt {{x_2}} + 3\sqrt {{x_1}} = 4\left( {\sqrt {{x_1}} + \sqrt {{x_2}} } \right) = 20.\) \[ab = \left( {\sqrt {{x_1}} + 3\sqrt {{x_2}} } \right).\left( {\sqrt {{x_2}} + 3\sqrt {{x_1}} } \right) = 10\sqrt {{x_1}.{x_2}} + 3({x_1} + {x_2}) = 10.3 + 3.19 = 87.\] Chú ý: Tính đúng một trong hai biểu thức tổng hoặc tích vẫn cho tối đa 0,25 điểm |
|
Vậy \(a,\,\,b\) là hai nghiệm của phương trình \({x^2} - 20x + 87 = 0.\) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập