Trong một cuộc tổng điều tra dân số, điều tra viên chọn ngẫu nhiên một gia đình có ba người con và quan tâm tới giới tính của ba người con này. Sơ đồ cây dưới đây mô tả các phần tử của không gian mẫu:

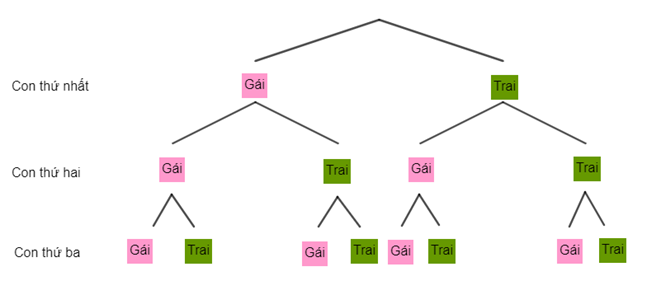
Số phần tử của không gian mẫu là

Hướng dẫn giải

Do \(n\) là số lẻ nên ta đặt \(n = 2k + 1\left( {k \in \mathbb{N},k \ge 1} \right)\).

Số phần tử không gian mẫu là:\(n\left( \Omega  \right) = C_{2k + 1}^3\).

Gọi \(A\) là biến cố: “\(3\) đỉnh được chọn tạo thành tam giác tù”

Giả sử tam giác \(ABC\) có góc \(\widehat A,\widehat B\) là góc  nhọn và  góc \(\widehat C\)  tù

Chọn một đỉnh bất kì làm đỉnh \(A\) có \(2k + 1\) cách

Khi đó còn lại \(2k\) đỉnh, từ điểm được chọn ta chia làm \(2\), mỗi bên là \(k\)  đỉnh

Để tạo thành tam giác tù thì \(2\) đỉnh còn lại phải được chọn từ \(k\) đỉnh cùng thuộc một phía so với điểm đã chọn do đó có \(C_k^2 + C_k^2\) cách chọn

Nhưng với cách tính như vậy số tam giác được lặp lại \(2\) lần nên

\(n\left( A \right) = \frac{{\left( {2k + 1} \right)\left( {C_k^2 + C_k^2} \right)}}{{2!}} = \left( {2k + 1} \right)C_k^2\)

Vậy \(P\left( A \right) = \frac{{\left( {2k + 1} \right)C_k^2}}{{C_{2k + 1}^3}} = \frac{{45}}{{62}}\).

\( \Leftrightarrow 62\frac{{k!}}{{2!\left( {k - 2} \right)!}}.\left( {2k + 1} \right) = 45\frac{{\left( {2k + 1} \right)!}}{{3!\left( {2k - 2} \right)!}}\)

\( \Leftrightarrow 62\frac{{k\left( {k - 1} \right)\left( {2k + 1} \right)}}{2} = 45\frac{{2k\left( {2k + 1} \right)\left( {2k - 1} \right)}}{6}\)

\( \Leftrightarrow 62{k^3} - 31{k^2} - 31k = 60{k^3} - 15k\)

\( \Leftrightarrow 2{k^3} - 31{k^2} - 16k = 0 \Leftrightarrow \left[ \begin{array}{l}k = 16\\k =  - \frac{1}{2}\\k = 0\end{array} \right.\).

Kết hợp với điều kiện \(k = 16\) thoả mãn bài toán.

Vậy \(n = 33\).

Hướng dẫn giải

Gọi số cần tìm có dạng \(\overline {{a_1}{a_2}{a_3}{a_4}{a_5}{a_6}} \) là số thỏa yêu cầu bài toán thì \({a_3} + {a_4} + {a_5} = 8\).

Có hai bộ \(3\) số có tổng bằng \(8\) trong các số \(1;2;3;...;9\) là: \(\left\{ {1;2;5} \right\}\)và \(\left\{ {1;3;4} \right\}\)

Nếu \({a_3};{a_4};{a_5} \in \left\{ {1;2;5} \right\}\) thì \({a_3},{a_4},{a_5}\) có \(3!\) cách chọn và \({a_1},{a_2},{a_6}\) có \(A_6^3\) cách chọn suy ra có \(3!A_6^3 = 720\) số thỏa mãn yêu cầu.

Nếu \({a_3};{a_4};{a_5} \in \left\{ {1;2;5} \right\}\) tương tự ta cũng có \(720\) số thỏa yêu cầu.

Vậy có \(720 + 720 = 1400\) số thỏa yêu cầu.

b) Điều kiện: \[n \ge 2,n \in {\mathbb{N}^*}\]

\[C_n^1 + C_n^2 = 15 \Leftrightarrow n + \frac{{n\left( {n - 1} \right)}}{2} = 15 \Leftrightarrow {n^2} + n - 30 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{n = 5}\\{n =  - 6}\end{array}} \right. \Rightarrow n = 5\]

Khi đó,

\[{\left( {x + \frac{2}{{{x^4}}}} \right)^5} = C_5^0{x^5}{\left( {\frac{2}{{{x^4}}}} \right)^0} + C_5^1{x^4}\left( {\frac{2}{{{x^4}}}} \right) + C_5^2{x^3}{\left( {\frac{2}{{{x^4}}}} \right)^2} + C_5^3{x^2}{\left( {\frac{2}{{{x^4}}}} \right)^3} + C_5^4x{\left( {\frac{2}{{{x^4}}}} \right)^4} + C_5^5{x^0}{\left( {\frac{2}{{{x^4}}}} \right)^5}\]\( = {x^5} + 10 + \frac{{40}}{{{x^5}}} + \frac{{80}}{{{x^{10}}}} + \frac{{80}}{{{x^{15}}}} + \frac{{32}}{{{x^{20}}}}\)

Suy hệ số của số hạng không chứa \[x\] trong khai triển \({\left( {x + \frac{2}{{{x^4}}}} \right)^5}\) là \(10\).