Tung một đồng xu cân đối một lần. Số phần tử của không gian mẫu là:

a) Không gian mẫu:

\[\left\{ {\left( {4;5} \right);\left( {4;6} \right);\left( {4;7} \right);\left( {5;4} \right);\left( {5;6} \right);\left( {5;7} \right);\left( {6;4} \right);\left( {6;5} \right);\left( {6;7} \right)} \right\}\]

Số kết quả thuận lợi của biến cố \[A\]: “Tổng hai số trên hai viên bi chia 3 dư 1” là:

\[\left\{ {\left( {4;6} \right);\left( {6;4} \right);\left( {6;7} \right);\left( {7;6} \right)} \right\}\]

Xác suất của biến cố \[A\] là \[P(A) = \frac{4}{{12}} = \frac{1}{3}\].

b) Gọi số xe thực tế tham gia chở hàng là \[x\](xe) \[x \in N*\]

Số xe dự định ban đầu là: \[x + 1\] (xe)

Dự kiến ban đầu mỗi xe chở số tấn hàng là: \[\frac{{66}}{{x + 1}}\](tấn)

Thực tế mỗi xe chở số tấn hàng là: \[\frac{{66}}{x}\] (tấn).

Theo bài ra ta có phương trình: \[\frac{{66}}{x} - \frac{{66}}{{x + 1}} = \frac{1}{2}\] hay \[{x^2} + x - 132 = 0\]

Giải ra ta có: \[{x_1} = 11\](thoả mãn); \[{x_2} =  - 12\](loại)

Vậy số xe thực tế tham gia chở hàng là: 11 (xe).

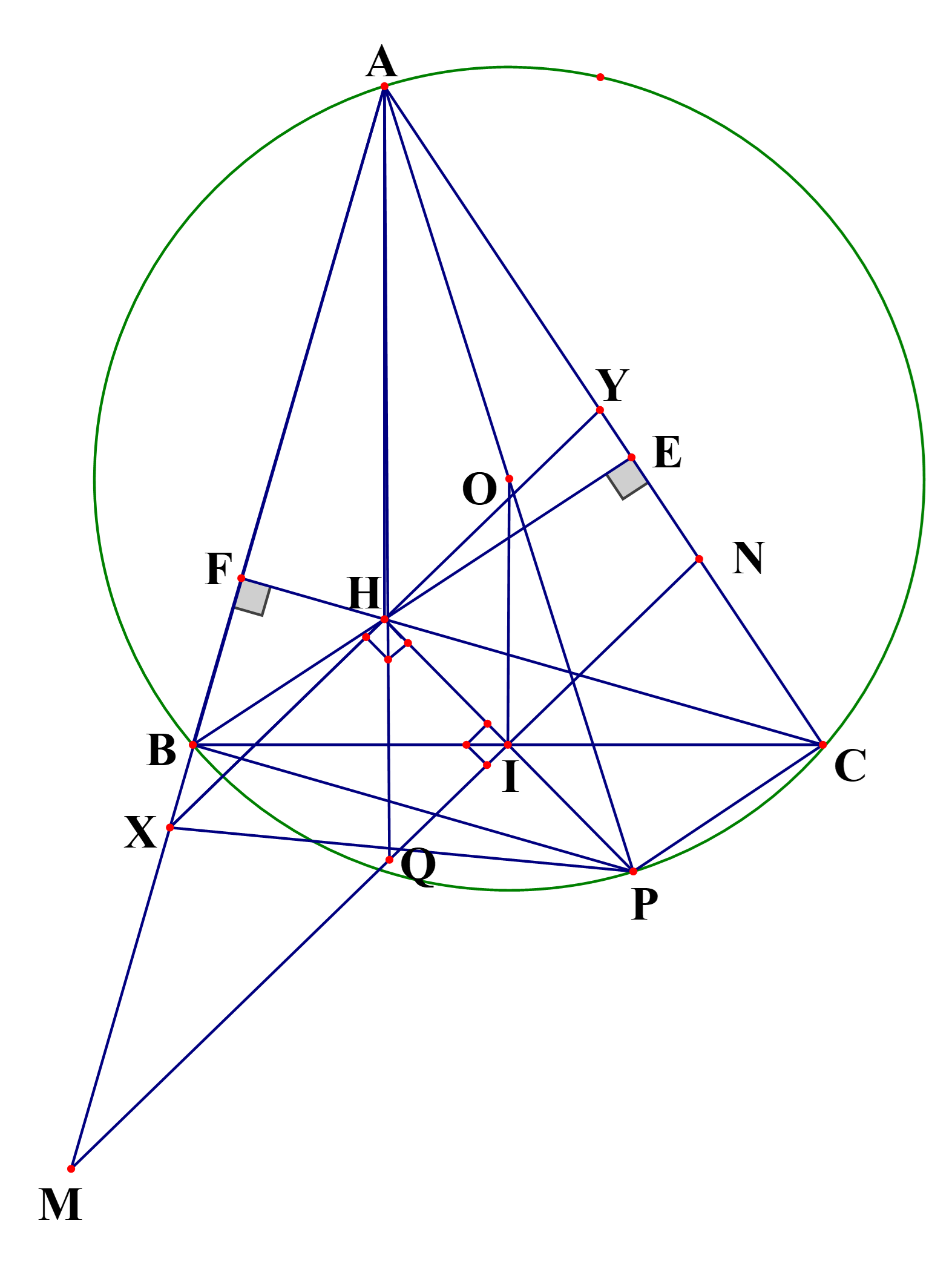
Suy ra 3 điểm \[B,E,C\] cùng nằm trên đường tròn đường kính BC (1).

Ta có: \[CF \bot AB\] nên \[\widehat {BFC} = 90^\circ .\]

Suy ra 3 điểm \[B,F,C\] cùng nằm trên đường tròn đường kính BC (2).

Từ (1) và (2) suy ra tứ giác \[BCEF\] nội tiếp.

b) Kẻ đường kính \[AP\] của đường tròn \[\left( O \right)\]. Khi đó \[PC \bot AC\] nên \[PC\]//\[BH\](cùng vuông góc với \[AC\]) và \[PB \bot AB\] nên \[PB\]//\[CH\](cùng vuông góc với \[AB\]). Do đó \[BHCP\] là hình bình hành.

Suy ra trung điểm \[I\]của \[BC\] cũng là trung điểm của \[PH\]. Vì vậy \[OI\] là đường trung bình của tam giác \[PAH\] nên \[OI = \frac{{AH}}{2}\] hay \[AH = 2OI\].

Kẻ đường thẳng qua \[H\], vuông góc với \[IH\]cắt các đường thẳng \[AB,AC\] lần lượt tại \[X,Y\].

Vì \[\widehat {PBX} = \widehat {PHX} = {90^o}\] nên các điểm \[P,B,X,H\] nằm trên đường tròn đường kính \[PX\], suy ra \[\widehat {PXH} = \widehat {PBH}\]. Tương tự \[\widehat {PCY} = \widehat {PHY} = {90^o}\] nên các điểm \[P,C,Y,H\] nằm trên đường tròn đường kính \[PY\], suy ra \[\widehat {PYH} = \widehat {PCH}\]

Mà \[BHCP\] là hình bình hành nên \[\widehat {PBH} = \widehat {PCH}\], suy ra \[\widehat {PXH} = \widehat {PYH}\] hay tam giác \[PXY\] cân tại \[P\], đường cao \[PH\] nên \[H\] là trung điểm của \[XY\].

Vì \[XY\]//\[MN\] nên ta có \[\frac{{XH}}{{MQ}} = \frac{{AH}}{{AQ}} = \frac{{HY}}{{QN}}\]. Suy ra \[MQ = QN\] hay \[Q\] là trung điểm của \[MN\]