Cho tam giác \(ABC\) \(\left( {AB < AC} \right)\) có các góc nhọn nội tiếp đường tròn \(\left( {O;R} \right)\). Các đường cao \(AK,\,BE,\,CF\) của tam giác \(ABC\) cắt nhau tại \(H\) và cắt đường tròn \(\left( {O;R} \right)\) tại các điểm lần lượt là \(M,\,N,\,P\) (\(M\) khác \(A\), \(N\) khác \(B\), \(P\) khác \(C\)).

1. Chứng minh \[EF\,{\rm{//}}\,PN.\] \(\)

2. Chứng minh diện tích tứ giác \(AEOF\) bằng \(\frac{{EF.R}}{2}.\)

3. Tính giá trị của biểu thức  \[\frac{{AM}}{{AK}} + \frac{{BN}}{{BE}} + \frac{{CP}}{{CF}}.\]

4. Gọi \(S\) và \(Q\) là chân đường vuông góc kẻ từ điểm \(K\) đến các cạnh \(AB,\,AC\). Đường thẳng \(QS\) cắt \(BC\) tại \(G\), đường thẳng \(GA\) cắt đường tròn \(\left( {O;R} \right)\) tại điểm \(J\)

(\(J\) khác \(A\)). Gọi \(I\) là tâm đường tròn ngoại tiếp tứ giác \(BCQS\). Chứng minh ba điểm \(I,\,K,\,J\) thẳng hàng.

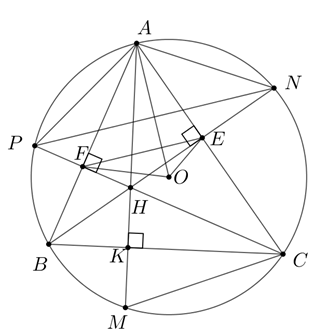
1.\(\widehat {BEC} = \widehat {BFC} = {90^0} \Rightarrow \) tứ giác \(BCEF\) nội tiếp đường tròn đường kính \(BC\)

\( \Rightarrow \widehat {CBE} = \widehat {CFE}\) ( góc nội tiếp cùng chắn cung )

Mà \(\widehat {CBE} = \widehat {CPN}\)( góc nội tiếp cùng chắn cung )

\( \Rightarrow \widehat {CFE} = \widehat {CPN} \Rightarrow EF\,//\,PN\,\)

2.\[\widehat {ABN} = \widehat {ACP}\] (cùng phụ với \(\widehat {BAC}\) )

\( \Rightarrow AN = AP\,\,\)

\(ON = OP = R\)

\( \Rightarrow A,\,O\)nằm trên đường trung trực của \(PN\)

\( \Rightarrow AO \bot PN\)

Mà \(EF\,//\,PN\, \Rightarrow AO \bot EF \Rightarrow {S_{AEOF}} = \frac{{EF.R}}{2}\)

3.\(\widehat {BAM} = \widehat {BCM}\) ( góc nội tiếp cùng chắn cung )

\(\widehat {BAM} = \widehat {BCF}\) (cùng phụ với \(\widehat {ABC}\))

\( \Rightarrow \widehat {BCF} = \widehat {BCM}\)

\(\Delta MCH\) có \(CK\) vừa là đường phân giác vừa là đường cao

\( \Rightarrow \)\(\Delta MCH\)cân tại \(C \Rightarrow K\) là trung điểm của \(MH\)

\[\begin{array}{l}\frac{{AM}}{{AK}} + \frac{{BN}}{{BE}} + \frac{{CP}}{{CF}} = \frac{{AK + KM}}{{AK}} + \frac{{BE + EN}}{{BE}} + \frac{{CF + FP}}{{CF}}\\ = 3 + \frac{{KM}}{{AK}} + \frac{{EN}}{{BE}} + \frac{{FP}}{{CF}}.\end{array}\]

\[\frac{{KM}}{{AK}} = \frac{{KH}}{{AK}} = \frac{{{S_{\Delta BHC}}}}{{{S_{\Delta ABC}}}}\]

Chứng minh tương tự: \[\frac{{EN}}{{BE}} = \frac{{{S_{\Delta AHC}}}}{{{S_{\Delta ABC}}}};\,\frac{{FP}}{{CF}} = \frac{{{S_{\Delta AHB}}}}{{{S_{\Delta ABC}}}}\]

\[\frac{{AM}}{{AK}} + \frac{{BN}}{{BE}} + \frac{{CP}}{{CF}} = 3 + \frac{{{S_{\Delta BHC}} + {S_{\Delta AHC}} + {S_{\Delta AHB}}}}{{{S_{\Delta ABC}}}} = 3 + 1 = 4.\]

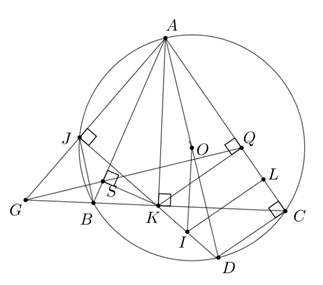
4.\[\widehat {ASK} + \widehat {AQK} = 90^\circ + 90^\circ = 180^\circ \] nên \[{\rm{AS}}KQ\] là tứ giác nội tiếp

\[ \Rightarrow \widehat {ASQ} = \widehat {AKQ}\]

\[\widehat {AKQ} = \widehat {BCQ}\] (cùng phụ với \(\widehat {CKQ}\) )

Do đó \[\widehat {ASQ} = \widehat {BCQ}\]

Suy ra \(BSQC\) là tứ giác nội tiếp.

\( \Rightarrow \widehat {GBS} = \widehat {GQC}\)

Vì \[ASKQ\]là tứ giác nội tiếp nên: \(\widehat {GQK} = \widehat {BAK}\)

Mà \(\widehat {BAK} = \widehat {GKS}\)(cùng phụ với \(\widehat {SBK}\)) nên \(\widehat {GQK} = \widehat {GKS}\)

Từ (1) và (2) \[ \Rightarrow G{K^2} = GB.GC\,\,\]

\[ \Rightarrow G{K^2} = GJ.GA \Rightarrow \frac{{GK}}{{GA}} = \frac{{GJ}}{{GK}}\]

⇒ $\Delta GKJ\backsim \Delta GAK\Rightarrow \widehat{GJK}=\widehat{GKA}=90°$

⇒ AJ ⊥ JK

 \(JK\) cắt \(\left( O \right)\) tại \(D\) (\(D\)khác \(K\)) thì \(AD\)là đường kính của \(\left( O \right)\).

Gọi \(I\) là trung điểm \(KD\), \(L\) là trung điểm \(QC\).

Khi đó \(OI\) là đường trung bình của \(\Delta AKD \Rightarrow OI{\rm{//}}AK \Rightarrow OI \bot BC\)

Mà \(OB = OC\) nên \(OI\) là trung trực \(BC\) (3)

Vì \(KQ{\rm{//}}DC\) (cùng vuông góc\(AC\)) nên \(KQCD\) là hình thang.

⇒ \(IL\) là đường trung bình của hình thang \(KQCD\)

⇒ \(IL{\rm{//}}KQ \Rightarrow IL \bot QC\)

⇒ \(IL\) là trung trực của \(QC\) (4)

Từ (3) và (4) ⇒ \(I\) là tâm đường tròn ngoại tiếp tứ giác \(BSQC\)

Vậy \(I,\,K,\,J\) thẳng hàng.