Cho biểu thức \(A = \frac{{x + 1}}{{\sqrt x  - 1}} - \frac{{x\sqrt x  + 1}}{{x - 1}}\,\left( {x \ge 0,{\rm{ }}x \ne 1} \right)\).

a) Rút gọn biểu thức \(A\).

b) Tính giá trị của biểu thức \(A\)khi \(x = 4\).

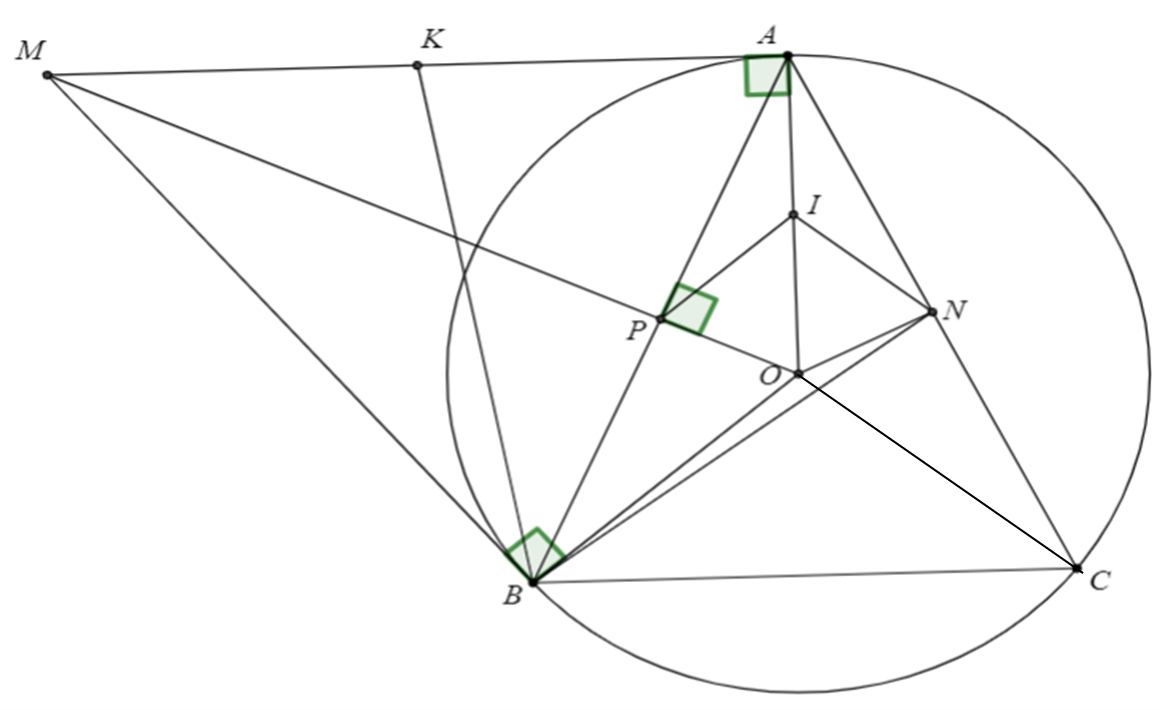
a) Vì \(MA,\,MB\) là hai tiếp tuyến cắt nhau tại \(M\) nên \(MA = MB\), suy ra \(M\) thuộc trung trực của \(AB\) \(\left( 1 \right)\).

Xét \(\left( O \right)\) có \(OA = OB\) suy ra \(O\) thuộc trung trực của \(AB\) \(\left( 2 \right)\).

Từ \(\left( 1 \right)\) và \(\left( 2 \right)\) suy ra \(OM\) là đường trung trực của \(AB\) hay \(OM \bot AB\) tại \(P\).

Ta có \(OA = OC\) suy ra \(\Delta AOC\) cân tại \(O\), khi đó \(ON \bot AC\) hay \(ON \bot AN\).

Gọi \(I\) là trung điểm của của \(OA\) mà các \(\Delta OPA\), \(\Delta ONA\) lần lượt vuông tại \(P,{\rm{ }}N\) nên ta có \(IP = IN = IA = IO = \frac{{OA}}{2}\).

Vậy bốn  điểm \(A,{\rm{ }}P,{\rm{ }}N,{\rm{ }}O\) cùng thuộc \(\left( {I;{\rm{ }}\frac{{AO}}{2}} \right)\).

b) Ta có \(MA = MB\) nên \(\widehat {MAB} = \widehat {MBA}\) \(\left( 3 \right)\)

Do \(\Delta ABC\)cân tại \(A\) nên \(\widehat {ABC} = \widehat {ACB}\) \(\left( 4 \right)\)

Xét \(\Delta MPA\) và \(\Delta MAO\) có:

\(\widehat {MPA} = \widehat {MAO} = 90^\circ \)

\(\widehat {AMO}\) chung

Suy ra \(\left( {{\rm{g}}{\rm{.g}}} \right)\).

Nên \(\widehat {MAB} = \widehat {MAP} = \widehat {MOA} = \frac{1}{2}\widehat {BOA}\) \(\left( 5 \right)\)

Mà \(\widehat C\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {ACB} = \frac{1}{2}\widehat {BOA}\) \(\left( 6 \right)\)

Từ \(\left( 3 \right)\), \(\left( 4 \right)\), \(\left( 5 \right)\), \(\left( 6 \right)\) suy ra \(\widehat {MAB} = \widehat {MBA} = \widehat {ACB} = \widehat {ABC}\).

Xét \(\Delta MAB\)và \(\Delta ACB\) có:

\(\widehat {MAB} = \widehat {ACB}\) (cmt)

\(\widehat {MBA} = \widehat {ABC}\) (cmt)

Suy ra \(\left( {g.g} \right)\).

Ta có \(\frac{{MB}}{{MA}} = \frac{{AB}}{{AC}}\) suy ra \(\frac{{MB}}{{2MK}} = \frac{{AB}}{{2AN}}\) nên \(\frac{{MB}}{{MK}} = \frac{{AB}}{{AN}}\).

Xét \(\Delta MBK\)và \(\Delta ABN\) có:

\(\widehat M = \widehat A\)

\(\frac{{MB}}{{MK}} = \frac{{AB}}{{AN}}\) (cmt)

Suy ra \(\left( {c.g.c} \right)\).

Khi đó \(\frac{{BM}}{{BK}} = \frac{{BA}}{{BN}}\)

Lại có \(BA = AC\) nên \(\frac{{BM}}{{BK}} = \frac{{CA}}{{BN}}\) hay \(BM{\rm{ }}.{\rm{ }}BN = CA\,\,.{\rm{ }}BK\).

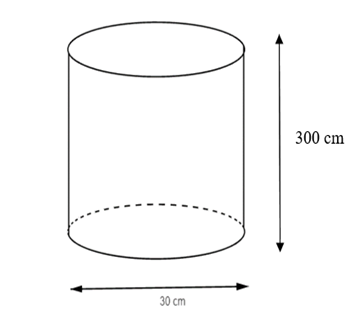
Ta có \(300\,{\rm{cm}} = 3\,{\rm{m}}\), \(30\,{\rm{cm}} = 0,3\,{\rm{m}}\).

Khi đó chiều cao \(h = 3\,{\rm{m}}\), bán kính đáy là \(R = 0,15\,{\rm{m}}\).

Ta có diện tích xung quanh là \({S_{xq}} = 2\pi Rh = 0,9\pi {\rm{ }}\left( {{m^2}} \right)\).

Chi phí là \(0,9\pi \,.\,200{\rm{ }}000 \approx 565{\rm{ 000}}\) (đồng).

Vậy bác Bình cần phải trả \(565{\rm{ 000}}\) đồng.