Cho biểu thức \[P = \left( {\frac{{\sqrt x  + 1}}{{\sqrt x  - 1}} - \frac{{\sqrt x  - 1}}{{\sqrt x  + 1}} - \frac{8}{{x - 1}}} \right) \cdot \frac{{x - 1}}{{\sqrt x }}\] với \[x > 0\] và \[x \ne 1\].

 1) Rút gọn biểu thức \[P\].

            2) Tìm tất cả các số nguyên \[x\] sao cho \[\left| P \right| + P = 0\].

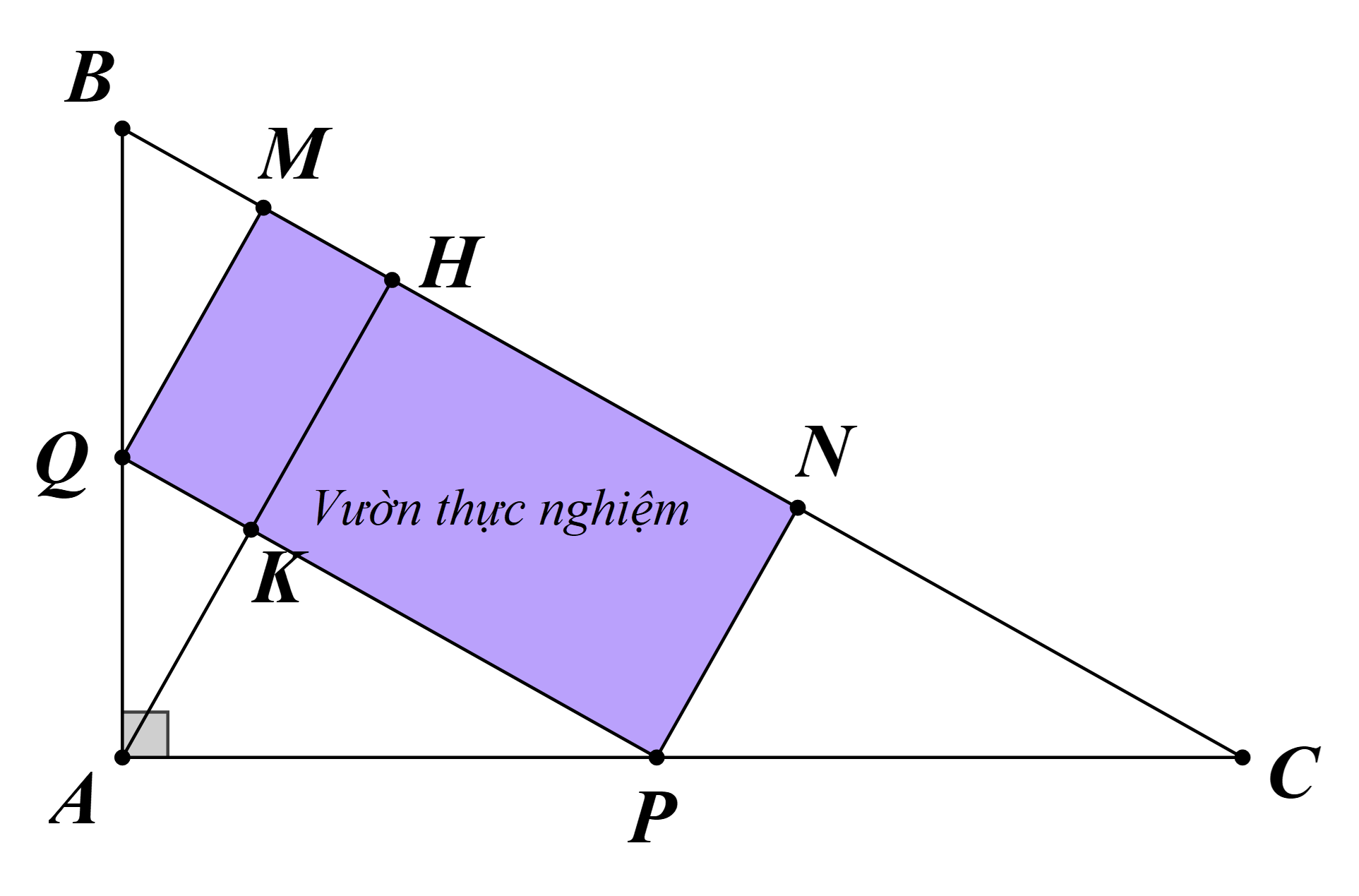
Hạ \[AH \bot BC\], gọi \[AH\] cắt \[PQ\] tại \[K\].

Ta có \[PQ{\rm{//}}BC\] nên \[QK{\rm{//}}BH\] và \[PK{\rm{//C}}H\] do đó \[\frac{{QK}}{{BH}} = \frac{{AK}}{{AH}} = \frac{{PK}}{{CH}} = \frac{{QK + PK}}{{BH + CH}} = \frac{{PQ}}{{BC}}\] (1)

Kí hiệu \[MQ = x,PQ = y\] thì \[KH = MQ = x\] (đk: \[x,y > 0\])

\[\Delta ABC\] vuông tại \[A\] nên \[B{C^2} = A{B^2} + A{C^2} = {6^2} + {8^2} = 100\] (định lý pytago) nên \[BC = 10\].

Khi đó: \[{S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.AH.BC\] nên \[AH = \frac{{AB.AC}}{{BC}} = \frac{{6.8}}{{10}} = \frac{{24}}{5}\]

Từ (1), ta có: \[\frac{{AK}}{{AH}} = \frac{{PQ}}{{BC}}\] nên \[1 - \frac{{KH}}{{AH}} = \frac{{PQ}}{{BC}}\]\[ \Rightarrow 1 - \frac{x}{{\frac{{24}}{5}}} = \frac{y}{{10}}\]

Hay \[1 = \frac{{5x}}{{24}} + \frac{y}{{10}} \ge 2\sqrt {\frac{{5x}}{{24}}.\frac{y}{{10}}} \]\[ \Rightarrow \frac{1}{4} \ge \frac{{xy}}{{48}}\] hay \[xy \le 12\]\[ \Rightarrow {S_{MNPQ}} = xy \le 12\]

Do đó, diện tích mảnh vườn thực nghiệm lớn nhất là: \[12\left( {{{\rm{m}}^{\rm{2}}}} \right)\].

Số tiền để nhà trường làm mảnh vườn có diện tích lớn nhất là: \[12.1,2 = 14,4\] (triệu đồng).

Xét phương trình \[{x^2} - 7x + 2 = 0\] có \[\Delta  = {\left( { - 7} \right)^2} - 4.2 = 41 > 0\] nên phương trình bài ra có hai nghiệm phân biệt \[{x_1},{x_2}\].

Áp dụng định lí Vi-ét, ta có: \[\left\{ \begin{array}{l}{x_1} + {x_2} = 7 > 0\\{x_1}.{x_2} = 2 > 0\end{array} \right.\] nên \[{x_1},{x_2}\] là hai nghiệm dương phân biệt.

Vì \[{x_2}\] là nghiệm phương trình \[{x^2} - 7x + 2 = 0\] nên ta có: \[x_2^2 - 7{x_2} + 2 = 0\] hay \[x_2^2 = 7{x_2} - 2\]

Suy ra: \[2x_2^2 - {x_2} + 11 = x_2^2 - {x_2} + 11 + x_2^2 = x_2^2 - {x_2} + 11 + 7{x_2} - 2\]\[ = x_2^2 + 6{x_2} + 9 = {\left( {{x_2} + 3} \right)^2}\]

Khi đó: \[T = \sqrt {{{\left( {{x_1} + 1} \right)}^2}}  + \sqrt {{{\left( {{x_2} + 3} \right)}^2}}  = \left| {{x_1} + 1} \right| + \left| {{x_2} + 3} \right|\]\[ = {x_1} + 1 + {x_2} + 3\] ( vì \[{x_1},{x_2} > 0 \Rightarrow {x_1} + 1 > 0,{x_2} + 3 > 0\]) hay \[T = {x_1} + {x_2} + 4 = 11\].

Vậy \[T = 11\].