Một xe bồn chở nước sạch cho một cụm dân cư có 100 hộ dân. Mỗi đầu của bồn chứa nước là nửa hình cầu, thân bồn chứa nước là hình trụ (có kích thước như hình vẽ). Bồn chứa đầy nước và lượng nước được chia đều cho từng hộ dân. Hỏi mỗi hộ dân nhận được bao nhiêu mét khối nước sạch? (kết quả làm tròn đến chữ số thập phân thứ hai, lấy \[\pi \approx 3,14\]).
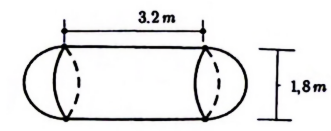
Một xe bồn chở nước sạch cho một cụm dân cư có 100 hộ dân. Mỗi đầu của bồn chứa nước là nửa hình cầu, thân bồn chứa nước là hình trụ (có kích thước như hình vẽ). Bồn chứa đầy nước và lượng nước được chia đều cho từng hộ dân. Hỏi mỗi hộ dân nhận được bao nhiêu mét khối nước sạch? (kết quả làm tròn đến chữ số thập phân thứ hai, lấy \[\pi \approx 3,14\]).

Quảng cáo
Trả lời:
Gọi \[{V_1}\] là thể tích phần hình trụ, khi đó
\[{V_1} = \pi {R^2}h = \pi {.0,9^2}.3,2 = 2,592\pi \,({m^3})\]
Gọi \[{V_2}\] là thể tích phần hai bán cầu, do mỗi đầu của bồn chứa nước là nửa hình cầu nên ta ghép lại được thành một hình cầu.
Khi đó \[{V_2} = \frac{4}{3}\pi {R^3} = \frac{4}{3}\pi {.0,9^3} = 0,972\pi \,({m^3})\].
Gọi \[V\] là thể tích của cả bồn, khi đó
\[V = {V_1} + {V_2} = 2,592\pi + 0,972\pi = 3,564\pi \,({m^3})\]
Thể tích nước của mỗi hộ dân nhận được là
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
a) Vì \[BK\] vuông góc với \[BC\] nên \[\widehat {BKC} = 90^\circ \]. Suy ra \[\Delta BKC\] nội tiếp đường tròn đường kính \[BC\]. |
|
Vì \[CN\] vuông góc với \[BC\] nên \[\widehat {BNC} = 90^\circ \]. Suy ra \[\Delta BNC\] nội tiếp đường tròn đường kính \[BC\]. |
|
Do đó, tứ giác \[BNKC\] nội tiếp đường tròn đường kính \[BC\]. |
|
Vì tứ giác \[BNKC\] nội tiếp đường tròn đường kính \[BC\](cmt) nên \[\widehat {ABH} = \widehat {NCA}\]\[(1)\] |
|
b) Vì \[CE\] vuông góc với \[AM\] nên \[\widehat {AEC} = 90^\circ \]. Suy ra \[\Delta AEC\] nội tiếp đường tròn đường kính \[AC\]. Vì \[CN\] vuông góc với \[AB\] nên \[\widehat {ANC} = 90^\circ \]. Suy ra \[\Delta ANC\] nội tiếp đường tròn đường kính \[AC\]. Do đó, tứ giác \[ANEC\] nội tiếp đường tròn đường kính \[BC\]. Suy ra \[\widehat {NEA} = \widehat {NCA}\]\[(2)\] |
|
Từ \[(1)\] và \[(2)\] suy ra \[\widehat {ABH} = \widehat {NEA}\]. |
|
Gọi \[P\] là trung điểm của \[BC\]. Dễ dàng chứng minh được \[OP\] vuông góc \[BC\]. Do đó \[\widehat {OPC} = 90^\circ \]. Mà \[\widehat {OEC} = \widehat {AEC} = 90^\circ \] nên \[OPEC\] nội tiếp đường tròn đường kính \[OC\]. Suy ra \[\widehat {PEO} = \widehat {PCO}\] \[(3)\] |
|
c) Xét \[\Delta OPC\] và \[\Delta ANC\] có \[\widehat {OPC} = \widehat {ANC} = 90^\circ \] \[\widehat {POC} = \widehat {NAC}\left( {\frac{1}{2}\widehat {BOC}} \right)\]
\[ \Rightarrow \widehat {PCO} = \widehat {NCA}\]\[(4)\] |
|
Từ \[(3)\] và \[(4)\] suy ra \[\widehat {PEO} = \widehat {ACN}\] \[(5)\] Từ \[(1)\] và \[(5)\] suy ra \[\widehat {NEA} = \widehat {PEO}\], suy ra \[N,P,E\] thẳng hàng. |
Lời giải
|
\[2{x^2} - 6x + 1 = 0\] (với \[a = 2;b = - 6;c = 1\]) Có \[\Delta = {( - 6)^2} - 4.2.1 = 28 > 0\] Do \[\Delta > 0\] nên phương trình đã cho có 2 nghiệm phân biệt Theo định lí Viète, ta có: \[\left\{ \begin{array}{l}{x_1} + {x_2} = 3\\{x_1}.{x_2} = \frac{1}{2}\end{array} \right.\] Khi đó \[B = x_1^2 + x_2^2 + 2025 = {({x_1} + {x_2})^2} - 2{x_1}{x_2} + 2025 = {3^2} - 2.\frac{1}{2} + 2025 = 2033\]. |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.