1) Giải phương trình: \(\frac{x}{{x + 2}} - \frac{2}{{{x^2} + 3x + 2}} = 0\).
2) Hai cây nến có cùng chiều dài và làm từ các chất liệu khác nhau, cây nến thứ nhất cháy hết với tốc độ đều trong 4 giờ, cây nến thứ nhất cháy hết với tốc độ đều trong 6 giờ. Hỏi nếu đốt cùng một lúc thì sau bao lâu phần còn lại của cây nến thứ hai gấp đôi phần còn lại của cây nến thứ nhất.
1) Giải phương trình: \(\frac{x}{{x + 2}} - \frac{2}{{{x^2} + 3x + 2}} = 0\).
2) Hai cây nến có cùng chiều dài và làm từ các chất liệu khác nhau, cây nến thứ nhất cháy hết với tốc độ đều trong 4 giờ, cây nến thứ nhất cháy hết với tốc độ đều trong 6 giờ. Hỏi nếu đốt cùng một lúc thì sau bao lâu phần còn lại của cây nến thứ hai gấp đôi phần còn lại của cây nến thứ nhất.
Quảng cáo
Trả lời:
Giải bởi Vietjack
1.ĐK: \[x \ne - 2;x \ne - 1\]
\[\frac{x}{{x + 2}} - \frac{2}{{{x^2} + 3x + 2}} = 0 \Leftrightarrow \frac{{x(x + 1)}}{{(x + 1)(x + 2)}} - \frac{2}{{(x + 1)(x + 2)}} = 0\].
.\[ \Rightarrow {x^2} + x - 2 = 0\]\[ \Leftrightarrow (x - 1)(x + 2) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1(TM)\\x = - 2(KTM)\end{array} \right.\]. KL….
2.Gọi thời gian đốt nến để phần còn lại của cây nến thứ 2 gấp đôi phần còn lại của cây nến thứ nhất là \[x(h);\,\,x > 0\] .
.Trong 1 giờ cây thứ nhất cháy hết \[\frac{1}{4}\]( cây)
Trong 1 giờ cây thứ hai cháy hết \[\frac{1}{6}\]( cây)
Phần còn lại của cây nến thứ nhất sau x giờ là \[\frac{{4 - x}}{4}\]( cây)
Phần còn lại của cây nến thứ hai sau x giờ là \[\frac{{6 - x}}{4}\]( cây).
.Theo bài ra ta có PT: \[\frac{{2(4 - x)}}{4} = \frac{{6 - x}}{6}\]
Giải phương trình ta được \[x = 3(TM)\]. KL…….
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
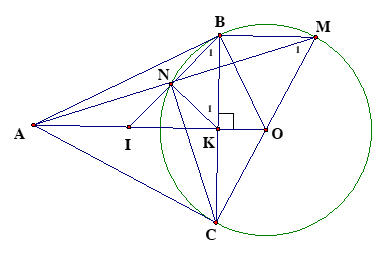
1.Ta có: \(\widehat {ABO} + \widehat {ACO} = 180^\circ \)\[\].
.\( \Rightarrow \) tứ giác ABOC nội tiếp.
2.Ta có: \(\widehat {BMN} = \widehat {NAI}\)( So le trong)
\(\widehat {ABN} = \widehat {BMN}\)( góc tạo bởi tia tiếp tuyến và góc nội tiếp cùng chắn cung BN) (1)
\( \Rightarrow \widehat {NAI} = \widehat {ABN}\).
.\( \Rightarrow \) Tam giác AIN đồng dạng với tam giác BIA\( \Rightarrow \frac{{AI}}{{NI}} = \frac{{IB}}{{AI}} \Rightarrow A{I^2} = IB.IN(*)\).
3.Ta có OB = OC, AB = AC \( \Rightarrow AO \bot BC\), mà BM//AO\( \Rightarrow BM \bot BC\)
\( \Rightarrow \widehat {CBM} = 90^\circ \Rightarrow M,O,C\) thẳng hàng
\( \Rightarrow \widehat {MNC} = 90^\circ {\rm{ }} \Rightarrow \widehat {ANC} = 90^\circ \)\( \Rightarrow \) tứ giác ANKC nội tiếp.
.\( \Rightarrow \widehat {CAN} = \widehat {{K_1}}\) mà \(\widehat {{B_1}} = \widehat {{M_1}}\)( góc nội tiếp cùng chắn cung NC)
\( \Rightarrow \widehat {{K_1}} + \widehat {{B_1}} = \widehat {CAN} + \widehat {{M_1}} = 90^\circ \Rightarrow \widehat {BNK} = 90^\circ \Rightarrow I{K^2} = IN.IB(**)\)
Từ (*) và (**)\(A{I^2} = I{K^2} \Rightarrow AI = IK\).
4.BM//AI \[ \Rightarrow \frac{{AM}}{{MN}} = \frac{{BI}}{{BN}}\]( Hệ quả của định lý Talet)
Mà \[\frac{{BI}}{{BN}} = \frac{{BI.BN}}{{B{N^2}}} = \frac{{K{B^2}}}{{B{N^2}}} \Rightarrow \frac{{AM}}{{MN}} = \frac{{K{B^2}}}{{B{N^2}}}\](3).
.BM//AI \[ \Rightarrow \frac{{MN}}{{AN}} = \frac{{BN}}{{NI}}\]( Hệ quả của định lý Talet)
\[\frac{{BN}}{{NI}} = \frac{{B{N^2}}}{{NI.BN}} = \frac{{B{N^2}}}{{N{K^2}}} \Rightarrow \frac{{MN}}{{AN}} = \frac{{B{N^2}}}{{N{K^2}}}\](4)
Từ (3) và (4) \[ \Rightarrow \frac{{AM}}{{AN}} = \frac{{K{B^2}}}{{K{N^2}}} = \frac{{K{C^2}}}{{K{N^2}}}(KB = KC)\]. Vậy \[\frac{{AM}}{{AN}} = \frac{{K{C^2}}}{{K{N^2}}}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
1.Xác định đúng 2 điểm thuộc đồ thị .
.Vẽ đúng đồ thị.
2.Tọa độ giao điểm của \(({d_1})\) và \(({d_2})\) là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}y = 2x - 5\\y = 3x - 2\end{array} \right.\].
.Giải hệ phương trình ta được: \[\left\{ \begin{array}{l}x = - 3\\y = - 11\end{array} \right.\]
Vậy tọa độ giao điểm của \(({d_1})\) và \(({d_2})\)là \(\left( { - 3; - 11} \right)\).
3.\[(\sqrt {10} - 1)\sqrt {11 + 2\sqrt {10} } = (\sqrt {10} - 1)\sqrt {{{(\sqrt {10} + 1)}^2}} \].
.\[ = (\sqrt {10} - 1)(\sqrt {10} + 1) = 10 - 1 = 9\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập