Đề thi tuyển sinh vào lớp 10 môn Toán chuyên năm 2021-2022 chuyên Hoàng Văn Thụ - Hòa Bình có đáp án
64 người thi tuần này 4.6 107 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
1.Xác định đúng 2 điểm thuộc đồ thị .
.Vẽ đúng đồ thị.
2.Tọa độ giao điểm của \(({d_1})\) và \(({d_2})\) là nghiệm của hệ phương trình \[\left\{ \begin{array}{l}y = 2x - 5\\y = 3x - 2\end{array} \right.\].
.Giải hệ phương trình ta được: \[\left\{ \begin{array}{l}x = - 3\\y = - 11\end{array} \right.\]
Vậy tọa độ giao điểm của \(({d_1})\) và \(({d_2})\)là \(\left( { - 3; - 11} \right)\).
3.\[(\sqrt {10} - 1)\sqrt {11 + 2\sqrt {10} } = (\sqrt {10} - 1)\sqrt {{{(\sqrt {10} + 1)}^2}} \].
.\[ = (\sqrt {10} - 1)(\sqrt {10} + 1) = 10 - 1 = 9\].
Lời giải
1.\[\left\{ \begin{array}{l}x + 2y = 4\\{x^2} + 3y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4 - 2y\\{(4 - 2y)^2} + 3y = 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4 - 2y\\4{y^2} - 13y + 9 = 0\end{array} \right.\].
.\[ \Leftrightarrow \left\{ \begin{array}{l}x = 4 - 2y\\4{y^2} - 13y + 9 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 4 - 2y\\\left[ \begin{array}{l}y = 1\\y = \frac{9}{4}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right.\\\left\{ \begin{array}{l}x = \frac{{ - 1}}{2}\\y = \frac{9}{4}\end{array} \right.\end{array} \right.\]
Vậy hệ phương trình có 2 nghiệm: \[(2;1),\left( {\frac{{ - 1}}{2};\frac{9}{4}} \right)\].
2.Hoành độ giao điểm của \((P)\) và \((d)\) là nghiệm phương trình \[2{x^2} = 4x - m + 1 \Leftrightarrow 2{x^2} - 4x + m - 1 = 0{\rm{ }}(1)\]
Để (d) cắt (P) tại hai điểm phân biệt thì phương trình (1) có 2 nghiệm phân biệt
Ta có \[{x_1}^2 + {x_2}^2 = 4{x_1}{x_2} \Leftrightarrow {({x_1} + {x_2})^2} = 6{x_1}{x_2}\]
Áp dụng hệ thức Vi-ét ta có:\[\left\{ \begin{array}{l}{x_1} + {x_2} = 2\\{x_1}{x_2} = \frac{{m - 1}}{2}\end{array} \right.\]
\[ \Rightarrow 4 = 3(m - 1)\]\[ \Leftrightarrow m = \frac{7}{3}(TM)\] . KL……….
Lời giải
1.ĐK: \[x \ne - 2;x \ne - 1\]
\[\frac{x}{{x + 2}} - \frac{2}{{{x^2} + 3x + 2}} = 0 \Leftrightarrow \frac{{x(x + 1)}}{{(x + 1)(x + 2)}} - \frac{2}{{(x + 1)(x + 2)}} = 0\].
.\[ \Rightarrow {x^2} + x - 2 = 0\]\[ \Leftrightarrow (x - 1)(x + 2) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1(TM)\\x = - 2(KTM)\end{array} \right.\]. KL….
2.Gọi thời gian đốt nến để phần còn lại của cây nến thứ 2 gấp đôi phần còn lại của cây nến thứ nhất là \[x(h);\,\,x > 0\] .
.Trong 1 giờ cây thứ nhất cháy hết \[\frac{1}{4}\]( cây)
Trong 1 giờ cây thứ hai cháy hết \[\frac{1}{6}\]( cây)
Phần còn lại của cây nến thứ nhất sau x giờ là \[\frac{{4 - x}}{4}\]( cây)
Phần còn lại của cây nến thứ hai sau x giờ là \[\frac{{6 - x}}{4}\]( cây).
.Theo bài ra ta có PT: \[\frac{{2(4 - x)}}{4} = \frac{{6 - x}}{6}\]
Giải phương trình ta được \[x = 3(TM)\]. KL…….
Lời giải
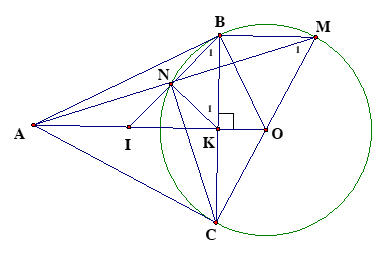
1.Ta có: \(\widehat {ABO} + \widehat {ACO} = 180^\circ \)\[\].
.\( \Rightarrow \) tứ giác ABOC nội tiếp.
2.Ta có: \(\widehat {BMN} = \widehat {NAI}\)( So le trong)
\(\widehat {ABN} = \widehat {BMN}\)( góc tạo bởi tia tiếp tuyến và góc nội tiếp cùng chắn cung BN) (1)
\( \Rightarrow \widehat {NAI} = \widehat {ABN}\).
.\( \Rightarrow \) Tam giác AIN đồng dạng với tam giác BIA\( \Rightarrow \frac{{AI}}{{NI}} = \frac{{IB}}{{AI}} \Rightarrow A{I^2} = IB.IN(*)\).
3.Ta có OB = OC, AB = AC \( \Rightarrow AO \bot BC\), mà BM//AO\( \Rightarrow BM \bot BC\)
\( \Rightarrow \widehat {CBM} = 90^\circ \Rightarrow M,O,C\) thẳng hàng
\( \Rightarrow \widehat {MNC} = 90^\circ {\rm{ }} \Rightarrow \widehat {ANC} = 90^\circ \)\( \Rightarrow \) tứ giác ANKC nội tiếp.
.\( \Rightarrow \widehat {CAN} = \widehat {{K_1}}\) mà \(\widehat {{B_1}} = \widehat {{M_1}}\)( góc nội tiếp cùng chắn cung NC)
\( \Rightarrow \widehat {{K_1}} + \widehat {{B_1}} = \widehat {CAN} + \widehat {{M_1}} = 90^\circ \Rightarrow \widehat {BNK} = 90^\circ \Rightarrow I{K^2} = IN.IB(**)\)
Từ (*) và (**)\(A{I^2} = I{K^2} \Rightarrow AI = IK\).
4.BM//AI \[ \Rightarrow \frac{{AM}}{{MN}} = \frac{{BI}}{{BN}}\]( Hệ quả của định lý Talet)
Mà \[\frac{{BI}}{{BN}} = \frac{{BI.BN}}{{B{N^2}}} = \frac{{K{B^2}}}{{B{N^2}}} \Rightarrow \frac{{AM}}{{MN}} = \frac{{K{B^2}}}{{B{N^2}}}\](3).
.BM//AI \[ \Rightarrow \frac{{MN}}{{AN}} = \frac{{BN}}{{NI}}\]( Hệ quả của định lý Talet)
\[\frac{{BN}}{{NI}} = \frac{{B{N^2}}}{{NI.BN}} = \frac{{B{N^2}}}{{N{K^2}}} \Rightarrow \frac{{MN}}{{AN}} = \frac{{B{N^2}}}{{N{K^2}}}\](4)
Từ (3) và (4) \[ \Rightarrow \frac{{AM}}{{AN}} = \frac{{K{B^2}}}{{K{N^2}}} = \frac{{K{C^2}}}{{K{N^2}}}(KB = KC)\]. Vậy \[\frac{{AM}}{{AN}} = \frac{{K{C^2}}}{{K{N^2}}}\].
Lời giải
1.Ta có \(P = ({a^4} + {b^4})({a^3} + {b^3}) - {a^3}{b^3}(a + b)\)
\(a + b = \sqrt 2 ;{\rm{ }}ab = \frac{1}{4} \Rightarrow \) \({a^3} + {b^3} = \frac{{5\sqrt 2 }}{4};{a^4} + {b^4} = \frac{{17}}{8}\).
.\( \Rightarrow P = \frac{{169\sqrt 2 }}{{64}}\).
2.Áp dụng BĐT AM-GM ta có : \(\frac{a}{{2\sqrt b - 5}} + 2\sqrt b - 5 \ge 2\sqrt a ;{\rm{ }}\frac{b}{{2\sqrt c - 5}} + 2\sqrt c - 5 \ge 2\sqrt {b;} {\rm{ }}\frac{c}{{2\sqrt a - 5}} + 2\sqrt a - 5 \ge 2\sqrt c \).
.\( \Rightarrow \frac{a}{{2\sqrt b - 5}} + \frac{b}{{2\sqrt c - 5}} + \frac{c}{{2\sqrt a - 5}} + 2\sqrt b - 5 + 2\sqrt c - 5 + 2\sqrt a - 5 \ge 2\sqrt b + 2\sqrt c + 2\sqrt a \)\( \Rightarrow Q \ge 15\)
Dấu “=” xảy ra khi và chỉ khi \(a = b = c = 25\).
\({Q_{\min }} = 15\) khi và chỉ khi \(a = b = c = 25\)..