Cho hai đường tròn \((O)\) và \(\left( {O'} \right)\) cắt nhau tại hai điểm \(A\) và \(B\). Tiếp tuyến tại \(A\) của đường tròn tâm \(O\) cắt đường tròn tâm \(O'\) tại \(P(P \ne A)\). Tiếp tuyến tại \(A\) của đường tròn tâm \(O'\) cắt đường tròn tâm \(O\) tại \(Q(Q \ne A)\). Gọi \(I\) là điểm sao cho tứ giác \(AOI{O^\prime }\) là hình bình hành và \(D\) đối xứng với \(A\) qua \(B\).
a) Chứng minh rằng \(I\) là tâm đường tròn ngoại tiếp tam giác \(APQ\). Từ đó suy ra tứ giác \(ADPQ\) nội tiếp?
b) Gọi \(M\) là trung điểm của đoạn \(PQ\). Chứng minh \(\widehat {ADP} = \widehat {QDM}\).
c) Giả sử hai đường thẳng \[IB\]và \[PQ\] cắt nhau tại \(S\). Gọi \(K\) là giao điểm của \[AD\] và \[PQ\]. Chứng minh:\(\frac{2}{{SK}} = \frac{1}{{SP}} + \frac{1}{{SQ}}\).\(\)
Cho hai đường tròn \((O)\) và \(\left( {O'} \right)\) cắt nhau tại hai điểm \(A\) và \(B\). Tiếp tuyến tại \(A\) của đường tròn tâm \(O\) cắt đường tròn tâm \(O'\) tại \(P(P \ne A)\). Tiếp tuyến tại \(A\) của đường tròn tâm \(O'\) cắt đường tròn tâm \(O\) tại \(Q(Q \ne A)\). Gọi \(I\) là điểm sao cho tứ giác \(AOI{O^\prime }\) là hình bình hành và \(D\) đối xứng với \(A\) qua \(B\).
a) Chứng minh rằng \(I\) là tâm đường tròn ngoại tiếp tam giác \(APQ\). Từ đó suy ra tứ giác \(ADPQ\) nội tiếp?
b) Gọi \(M\) là trung điểm của đoạn \(PQ\). Chứng minh \(\widehat {ADP} = \widehat {QDM}\).
c) Giả sử hai đường thẳng \[IB\]và \[PQ\] cắt nhau tại \(S\). Gọi \(K\) là giao điểm của \[AD\] và \[PQ\]. Chứng minh:\(\frac{2}{{SK}} = \frac{1}{{SP}} + \frac{1}{{SQ}}\).\(\)
Quảng cáo
Trả lời:
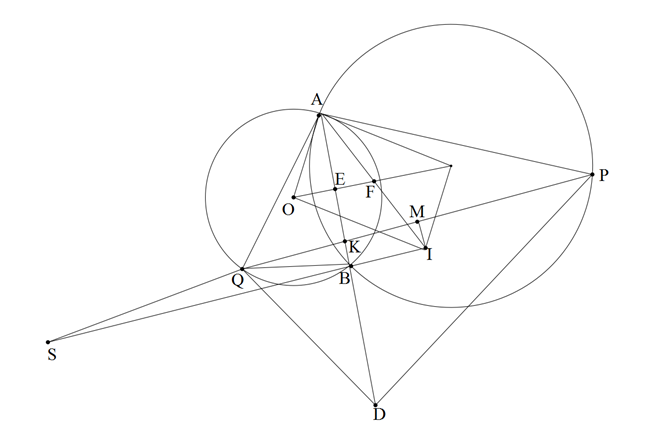
a) Ta có: \(OA \bot AP\) mà \(IO'//OA \Rightarrow IO' \bot AP \Rightarrow I'\) nằm trên đường trung trực của \(AP \Rightarrow IA = IP\). Chứng minh tương tự ta cũng có: \(IA = IQ\).
Từ đó suy ra: \(IA = IP = IQ \Rightarrow I\) là tâm đường tròn ngoại tiếp tam giác \(APQ\).
Gọi \(E,F\) lần lượt là giao điểm của \(OO'\) với \(AB\) và \(AI.\) Ta có:
Dễ thấy \(E,F\) lần lượt là trung điểm của \(AB\) và \(AI \Rightarrow EF\) là đường trung bình của tam giác \(ABI\).
Suy ra \(EF//BI\) hay \(OO//BI\). Do đó \(BI \bot AB\) tại \(B\).
Từ đó \(IB\) là đường trung trực của \(AD \Rightarrow IA = ID\).
Do đó tứ giác \(ADPQ\) nối tiếp.
b) Ta có: \(\widehat {QPD} = \widehat {QAD} = \widehat {QAB} = \widehat {APB} = \frac{1}{2}\widehat {AO'B} = \widehat {AO'O}\), hay \(\widehat {QPD} = \widehat {AO'O}\)
Chứng minh tương tự ta cũng có: \(\widehat {PQD} = \widehat {AOO'}\).
Từ đó suy ra
Mà \(M\) là trung điểm của \(PQ\) và \(F\) là trung điểm của \(OO' \Rightarrow \widehat {QDM} = \widehat {OAF}\).
Mặt khác \(\widehat {ADP} = \frac{1}{2}\widehat {AIP} = \widehat {AIO'} = \widehat {OAF}\).
Từ đây suy ra: \(\widehat {APD} = \widehat {QDM}\).
c) Theo chứng minh trên ta có: \(\widehat {QPD} = \widehat {QAB}\).
Mặt khác \(\widehat {DQP} = \widehat {DAP} = \widehat {AQB}\), hay \(\widehat {DQP} = \widehat {AQB}\)
Từ đó suy ra .
Suy ra:
\(\begin{array}{l}\widehat {QBI} + \widehat {IPQ} = \widehat {QBA} + \widehat {ABI} + \widehat {IPQ} = \widehat {QDP} + 90^\circ + \widehat {IPQ}\\ = \widehat {QPD} + 90^\circ + \frac{{180^\circ - \widehat {QIP}}}{2} = 180^\circ + \widehat {QPD} - \widehat {QDP} = 180^\circ \end{array}\)
Do đó tứ giác \(QBIP\) nội tiếp. Suy ra: \(SQ \cdot SP = SB \cdot SI\)
Vì \(M\) là trung điểm của đoạn \(PQ \Rightarrow IM \bot PQ \Rightarrow \) tứ giác \(BKMI\) nội tiếp.
Suy ra: \(SK \cdot SM = SB \cdot SI\).
Tu đó ta suy: \(SQ \cdot SP = SK \cdot SM \Leftrightarrow \frac{1}{{SK}} = \frac{{SM}}{{SQ \cdot SP}}\)
Mà \(SM = SP - MP = SP - MQ = SP - (SM - SQ) = SP + SQ - SM \Rightarrow SP + SQ = 2SM\)
Nên ta có: \(\frac{1}{{SK}} = \frac{{SM}}{{SQ \cdot SP}} \Leftrightarrow \frac{2}{{SK}} = \frac{{2SM}}{{SQ \cdot SP}} \Leftrightarrow \frac{2}{{SK}} = \frac{{SQ + SP}}{{SQ \cdot SP}} \Leftrightarrow \frac{2}{{SK}} = \frac{1}{{SQ}} + \frac{1}{{SP}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có: \((a + 2)(b + 2) = 8 \Leftrightarrow 2a + 2b + ab = 4\).
Do đó:
\[\begin{array}{*{20}{l}}{\sqrt {2\left( {{a^2} + 4} \right)\left( {{b^2} + 4} \right)} = \sqrt {2\left( {{a^2} + ab + 2a + 2b} \right)\left( {{b^2} + ab + 2a + 2b} \right)} }\\{ = \sqrt {2{{(a + b)}^2}(a + 2)(b + 2)} = \sqrt {2{{(a + b)}^2} \cdot 8} = 4(a + b).}\end{array}\]
Suy ra:
\(\begin{array}{*{20}{l}}{2\sqrt {{a^2} + {b^2} + 8 - \sqrt {2\left( {{a^2} + 4} \right)\left( {{b^2} + 4} \right)} } = 2\sqrt {{a^2} + {b^2} + 8 - 4(a + b)} }\\{ = 2\sqrt {{{(a + b)}^2} + 8 - 4(a + b) - 2ab} = 2\sqrt {{{(a + b)}^2}} = 2(a + b).}\end{array}\)
Khi đó: \(P = ab + 2(a + b) = 4\).
Vậy \(P = 4\).
b) Đặt \(x = a - b,y = b - c,z = c - a \Rightarrow x,y,z \ne 0\) và \(x + y + z = 0\).
Ta có:
\[\begin{array}{*{20}{l}}{B = \sqrt {\frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} + \frac{1}{{{z^2}}}} = \sqrt {{{\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right)}^2} - 2\left( {\frac{1}{{xy}} + \frac{1}{{yz}} + \frac{1}{{zx}}} \right)} = \sqrt {{{\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right)}^2} - \frac{{2(x + y + z)}}{{xyz}}} }\\{ = \sqrt {{{\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right)}^2}} = \left| {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right|}\end{array}\]
Vì \[a,b,c\]là các số hữu tỷ nên \[x,y,z\]là các số hữu tỉ, do đó \(B\) là số hữu tỷ.
Lời giải
a) Ta có:
\(\begin{array}{*{20}{l}}{{x^2} + 2{y^2} - 2xy - 2x - 4y + 6 = 0}\\{ \Leftrightarrow \left( {{x^2} + {y^2} + 1 - 2xy - 2x + 2y} \right) + \left( {{y^2} - 6y + 9} \right) = 4}\\{ \Leftrightarrow {{(x - y - 1)}^2} + {{(y - 3)}^2} = 4}\\{{\rm{ V\`i }}x,y \in \mathbb{Z} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{{(x - y - 1)}^2} = 4}\\{{{(y - 3)}^2} = 0}\end{array}\quad {\rm{ hoac }}\left\{ {\begin{array}{*{20}{l}}{{{(x - y - 1)}^2} = 0}\\{{{(y - 3)}^2} = 4}\end{array}} \right.} \right.}\end{array}\)
Trường hợp: \(\left\{ {\begin{array}{*{20}{l}}{{{(x - y - 1)}^2} = 4}\\{{{(y - 3)}^2} = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{(x - 4)}^2} = 4}\\{y = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 6}\\{y = 3}\end{array}} \right.} \right.} \right.\) hoặc \(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 3}\end{array}} \right.\).
Trường hợp: \(\left\{ {\begin{array}{*{20}{l}}{{{(x - y - 1)}^2} = 0}\\{{{(y - 3)}^2} = 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = y + 1}\\{y = 5}\\{y = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 6}\\{y = 5}\end{array}} \right.} \right.} \right.\) hoặc \(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 1}\end{array}} \right.\).
Vậy phương trình đã cho có bốn nghiệm \((x;y) = (6;3),(2;3),(6;5),(2;1)\).
b) Ta có: \(\frac{{{p^2} - p}}{2} - 1 = {a^3}\) với \(a \ge 0\). Khi đó:
\(\frac{{{p^2} - p}}{2} - 1 = {a^3} \Leftrightarrow p(p - 1) = 2(a + 1)\left( {{a^2} - a + 1} \right).\)Vì ưcln \((p;p - 1) = 1\) nên \(p(p - 1)\) chia hết cho \((a + 1) \Leftrightarrow p\) chia hết cho \((a + 1)\) hoặc \(p - 1\) chia hết cho \((a + 1)\).
- Xét \(p:(a + 1) \Rightarrow p = k(a + 1)\). Mà \(p\) là số nguyên tố suy ra: \(\left[ {\begin{array}{*{20}{l}}{k = 1}\\{a + 1 = 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{k = 1}\\{a = 0}\end{array}} \right.} \right.\).
Với \(a = 0 \Rightarrow p = 2\).
Nếu \(k = 1 \Rightarrow p = a + 1 \Rightarrow a(a + 1) = 2(a + 1)\left( {{a^2} - a + 1} \right)\), vô nghiệm.
Xét \(p - 1:(a + 1) \Rightarrow p = m(a + 1) + 1\). Khi đó ta có:
\(m(a + 1)p = 2(a + 1)\left( {{a^2} - a + 1} \right) \Leftrightarrow mp = 2\left( {{a^2} - a + 1} \right){\rm{ }}{\rm{. }}\)Ta có: \({a^2} - a + 1 = a(a - 1) + 1\) là một số lẽ. Suy ra: ưcln \(\left( {2;{a^2} - a + 1} \right) = 1\).
Nên \(2\left( {{a^2} - a + 1} \right):m \Leftrightarrow 2:m\) hoặc \(\left( {{a^2} - a + 1} \right):m\).
Nếu \(2:m \Rightarrow \left[ {\begin{array}{*{20}{l}}{m = 1}\\{m = 2}\end{array}} \right.\).
Với \(k = 1 \Rightarrow 2\left( {{a^2} - a + 1} \right) = a + 2 \Leftrightarrow 2{a^2} - 3a = 0 \Leftrightarrow a = 0\)
Với \(k = 2 \Rightarrow {a^2} - a + 1 = 2(a + 1) + 1 \Leftrightarrow {a^2} - 3a - 1 = 0\), vô nghiệm.
Nếu \({a^2} - a + 1:m \Rightarrow {a^2} - a + 1 = mn\). Khi đó ta có: \(m(a + 1) + 1 = 2n\).
Mặt khác \(p = m(a + 1) + 1 = 2n\) là số nguyên tố suy ra \(p = 2,n = 1 \Rightarrow a = 0\).
Tóm lại \(p = 2\) là số nguyên tố cần tìm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
