Đề thi tuyển sinh vào lớp 10 môn Toán chuyên năm 2021-2022 chuyên Lam Sơn - Thanh Hóa có đáp án
46 người thi tuần này 4.6 90 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 Toán (chung) Sở GD&ĐT Lạng Sơn lần 1 năm 2026-2027 có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chuyên) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề minh họa thi vào lớp 10 môn Toán (chung) năm 2026 Sở GD&ĐT Đồng Tháp có đáp án
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a) Ta có: \((a + 2)(b + 2) = 8 \Leftrightarrow 2a + 2b + ab = 4\).
Do đó:
\[\begin{array}{*{20}{l}}{\sqrt {2\left( {{a^2} + 4} \right)\left( {{b^2} + 4} \right)} = \sqrt {2\left( {{a^2} + ab + 2a + 2b} \right)\left( {{b^2} + ab + 2a + 2b} \right)} }\\{ = \sqrt {2{{(a + b)}^2}(a + 2)(b + 2)} = \sqrt {2{{(a + b)}^2} \cdot 8} = 4(a + b).}\end{array}\]
Suy ra:
\(\begin{array}{*{20}{l}}{2\sqrt {{a^2} + {b^2} + 8 - \sqrt {2\left( {{a^2} + 4} \right)\left( {{b^2} + 4} \right)} } = 2\sqrt {{a^2} + {b^2} + 8 - 4(a + b)} }\\{ = 2\sqrt {{{(a + b)}^2} + 8 - 4(a + b) - 2ab} = 2\sqrt {{{(a + b)}^2}} = 2(a + b).}\end{array}\)
Khi đó: \(P = ab + 2(a + b) = 4\).
Vậy \(P = 4\).
b) Đặt \(x = a - b,y = b - c,z = c - a \Rightarrow x,y,z \ne 0\) và \(x + y + z = 0\).
Ta có:
\[\begin{array}{*{20}{l}}{B = \sqrt {\frac{1}{{{x^2}}} + \frac{1}{{{y^2}}} + \frac{1}{{{z^2}}}} = \sqrt {{{\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right)}^2} - 2\left( {\frac{1}{{xy}} + \frac{1}{{yz}} + \frac{1}{{zx}}} \right)} = \sqrt {{{\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right)}^2} - \frac{{2(x + y + z)}}{{xyz}}} }\\{ = \sqrt {{{\left( {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right)}^2}} = \left| {\frac{1}{x} + \frac{1}{y} + \frac{1}{z}} \right|}\end{array}\]
Vì \[a,b,c\]là các số hữu tỷ nên \[x,y,z\]là các số hữu tỉ, do đó \(B\) là số hữu tỷ.
Lời giải
a) Do \[x = 0\]không là nghiệm của phương trình nên phương trình đã cho tương đương:
\(\begin{array}{l}(x + 1)(x + 2)(x + 3)(x + 6) = 168{x^2}\\ \Leftrightarrow \left( {{x^2} + 7x + 6} \right)\left( {{x^2} + 5x + 6} \right) = 168{x^2}\\ \Leftrightarrow \left( {x + \frac{6}{x} + 7} \right)\left( {x + \frac{6}{x} + 5} \right) = 168\\ \Leftrightarrow {\left( {x + \frac{6}{x}} \right)^2} + 12\left( {x + \frac{6}{x}} \right) + 35 = 168\\ \Leftrightarrow {\left( {x + \frac{6}{x}} \right)^2} + 12\left( {x + \frac{6}{x}} \right) - 133 = 0\end{array}\)\(\begin{array}{l} \Leftrightarrow \left( {x + \frac{6}{x} - 7} \right)\left( {x + \frac{6}{x} + 19} \right) = 0 \Leftrightarrow \left( {{x^2} - 7x + 6} \right)\left( {{x^2} - 19x + 6} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{x^2} - 7x + 6 = 0}\\{{x^2} + 19x + 6 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = 1}\\{x = 6}\end{array}} \right.} \right.x = - \frac{{\sqrt {337} - 19}}{2}.x = \frac{{\sqrt {337} + 19}}{2}\end{array}\)
Vậy tập nghiệm của phương trình \(S = \left\{ {1;6;\frac{{\sqrt {337} - 19}}{2}; - \frac{{\sqrt {337} + 19}}{2}} \right\}\).
b) Điều kiện \[y > 0\]. Phương trình thứ nhất của hệ tương đương:
\(\begin{array}{*{20}{l}}{x - y + \frac{1}{{{x^2} + 1}} - \frac{1}{{{y^2} + 1}} = 0 \Leftrightarrow x - y - \frac{{(x - y)(x + y)}}{{\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right)}} = 0}\\{ \Leftrightarrow (x - y)\left[ {1 - \frac{{x + y}}{{\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right)}}} \right] = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = y}\\{\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right) = x + y}\end{array}} \right.}\end{array}\)
Ta có:
\(\left( {{x^2} + 1} \right)\left( {{y^2} + 1} \right) = x + y \Leftrightarrow {x^2} - x + {y^2} - y + {x^2}{y^2} + 1 = 0\)
\( \Leftrightarrow {\left( {x - \frac{1}{2}} \right)^2} + {\left( {y - \frac{1}{2}} \right)^2} + {x^2}{y^2} + \frac{1}{2} = 0\), vô lí.
Do đó trong trường hợp này hệ phương trình vô nghiệm.
Vậy hệ đã cho có hai nghiệm: \((x;y) = (2 + \sqrt 3 ;2 + \sqrt 3 ),(2 - \sqrt 3 ;2 - \sqrt 3 )\).
Lời giải
a) Ta có:
\(\begin{array}{*{20}{l}}{{x^2} + 2{y^2} - 2xy - 2x - 4y + 6 = 0}\\{ \Leftrightarrow \left( {{x^2} + {y^2} + 1 - 2xy - 2x + 2y} \right) + \left( {{y^2} - 6y + 9} \right) = 4}\\{ \Leftrightarrow {{(x - y - 1)}^2} + {{(y - 3)}^2} = 4}\\{{\rm{ V\`i }}x,y \in \mathbb{Z} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{{(x - y - 1)}^2} = 4}\\{{{(y - 3)}^2} = 0}\end{array}\quad {\rm{ hoac }}\left\{ {\begin{array}{*{20}{l}}{{{(x - y - 1)}^2} = 0}\\{{{(y - 3)}^2} = 4}\end{array}} \right.} \right.}\end{array}\)
Trường hợp: \(\left\{ {\begin{array}{*{20}{l}}{{{(x - y - 1)}^2} = 4}\\{{{(y - 3)}^2} = 0}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{{{(x - 4)}^2} = 4}\\{y = 3}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 6}\\{y = 3}\end{array}} \right.} \right.} \right.\) hoặc \(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 3}\end{array}} \right.\).
Trường hợp: \(\left\{ {\begin{array}{*{20}{l}}{{{(x - y - 1)}^2} = 0}\\{{{(y - 3)}^2} = 4}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = y + 1}\\{y = 5}\\{y = 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x = 6}\\{y = 5}\end{array}} \right.} \right.} \right.\) hoặc \(\left\{ {\begin{array}{*{20}{l}}{x = 2}\\{y = 1}\end{array}} \right.\).
Vậy phương trình đã cho có bốn nghiệm \((x;y) = (6;3),(2;3),(6;5),(2;1)\).
b) Ta có: \(\frac{{{p^2} - p}}{2} - 1 = {a^3}\) với \(a \ge 0\). Khi đó:
\(\frac{{{p^2} - p}}{2} - 1 = {a^3} \Leftrightarrow p(p - 1) = 2(a + 1)\left( {{a^2} - a + 1} \right).\)Vì ưcln \((p;p - 1) = 1\) nên \(p(p - 1)\) chia hết cho \((a + 1) \Leftrightarrow p\) chia hết cho \((a + 1)\) hoặc \(p - 1\) chia hết cho \((a + 1)\).
- Xét \(p:(a + 1) \Rightarrow p = k(a + 1)\). Mà \(p\) là số nguyên tố suy ra: \(\left[ {\begin{array}{*{20}{l}}{k = 1}\\{a + 1 = 1}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{k = 1}\\{a = 0}\end{array}} \right.} \right.\).
Với \(a = 0 \Rightarrow p = 2\).
Nếu \(k = 1 \Rightarrow p = a + 1 \Rightarrow a(a + 1) = 2(a + 1)\left( {{a^2} - a + 1} \right)\), vô nghiệm.
Xét \(p - 1:(a + 1) \Rightarrow p = m(a + 1) + 1\). Khi đó ta có:
\(m(a + 1)p = 2(a + 1)\left( {{a^2} - a + 1} \right) \Leftrightarrow mp = 2\left( {{a^2} - a + 1} \right){\rm{ }}{\rm{. }}\)Ta có: \({a^2} - a + 1 = a(a - 1) + 1\) là một số lẽ. Suy ra: ưcln \(\left( {2;{a^2} - a + 1} \right) = 1\).
Nên \(2\left( {{a^2} - a + 1} \right):m \Leftrightarrow 2:m\) hoặc \(\left( {{a^2} - a + 1} \right):m\).
Nếu \(2:m \Rightarrow \left[ {\begin{array}{*{20}{l}}{m = 1}\\{m = 2}\end{array}} \right.\).
Với \(k = 1 \Rightarrow 2\left( {{a^2} - a + 1} \right) = a + 2 \Leftrightarrow 2{a^2} - 3a = 0 \Leftrightarrow a = 0\)
Với \(k = 2 \Rightarrow {a^2} - a + 1 = 2(a + 1) + 1 \Leftrightarrow {a^2} - 3a - 1 = 0\), vô nghiệm.
Nếu \({a^2} - a + 1:m \Rightarrow {a^2} - a + 1 = mn\). Khi đó ta có: \(m(a + 1) + 1 = 2n\).
Mặt khác \(p = m(a + 1) + 1 = 2n\) là số nguyên tố suy ra \(p = 2,n = 1 \Rightarrow a = 0\).
Tóm lại \(p = 2\) là số nguyên tố cần tìm.
Lời giải
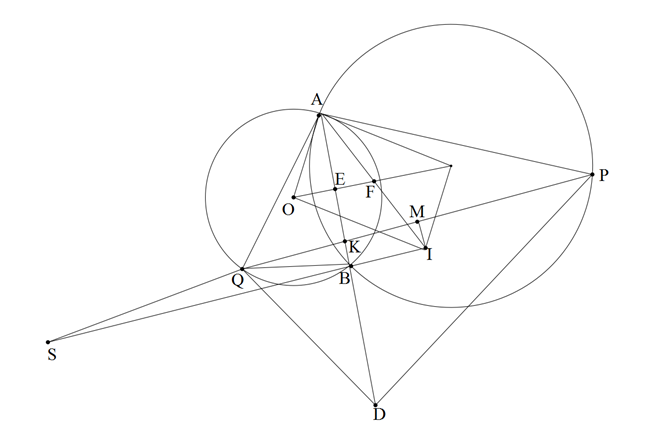
a) Ta có: \(OA \bot AP\) mà \(IO'//OA \Rightarrow IO' \bot AP \Rightarrow I'\) nằm trên đường trung trực của \(AP \Rightarrow IA = IP\). Chứng minh tương tự ta cũng có: \(IA = IQ\).
Từ đó suy ra: \(IA = IP = IQ \Rightarrow I\) là tâm đường tròn ngoại tiếp tam giác \(APQ\).
Gọi \(E,F\) lần lượt là giao điểm của \(OO'\) với \(AB\) và \(AI.\) Ta có:
Dễ thấy \(E,F\) lần lượt là trung điểm của \(AB\) và \(AI \Rightarrow EF\) là đường trung bình của tam giác \(ABI\).
Suy ra \(EF//BI\) hay \(OO//BI\). Do đó \(BI \bot AB\) tại \(B\).
Từ đó \(IB\) là đường trung trực của \(AD \Rightarrow IA = ID\).
Do đó tứ giác \(ADPQ\) nối tiếp.
b) Ta có: \(\widehat {QPD} = \widehat {QAD} = \widehat {QAB} = \widehat {APB} = \frac{1}{2}\widehat {AO'B} = \widehat {AO'O}\), hay \(\widehat {QPD} = \widehat {AO'O}\)
Chứng minh tương tự ta cũng có: \(\widehat {PQD} = \widehat {AOO'}\).
Từ đó suy ra
Mà \(M\) là trung điểm của \(PQ\) và \(F\) là trung điểm của \(OO' \Rightarrow \widehat {QDM} = \widehat {OAF}\).
Mặt khác \(\widehat {ADP} = \frac{1}{2}\widehat {AIP} = \widehat {AIO'} = \widehat {OAF}\).
Từ đây suy ra: \(\widehat {APD} = \widehat {QDM}\).
c) Theo chứng minh trên ta có: \(\widehat {QPD} = \widehat {QAB}\).
Mặt khác \(\widehat {DQP} = \widehat {DAP} = \widehat {AQB}\), hay \(\widehat {DQP} = \widehat {AQB}\)
Từ đó suy ra .
Suy ra:
\(\begin{array}{l}\widehat {QBI} + \widehat {IPQ} = \widehat {QBA} + \widehat {ABI} + \widehat {IPQ} = \widehat {QDP} + 90^\circ + \widehat {IPQ}\\ = \widehat {QPD} + 90^\circ + \frac{{180^\circ - \widehat {QIP}}}{2} = 180^\circ + \widehat {QPD} - \widehat {QDP} = 180^\circ \end{array}\)
Do đó tứ giác \(QBIP\) nội tiếp. Suy ra: \(SQ \cdot SP = SB \cdot SI\)
Vì \(M\) là trung điểm của đoạn \(PQ \Rightarrow IM \bot PQ \Rightarrow \) tứ giác \(BKMI\) nội tiếp.
Suy ra: \(SK \cdot SM = SB \cdot SI\).
Tu đó ta suy: \(SQ \cdot SP = SK \cdot SM \Leftrightarrow \frac{1}{{SK}} = \frac{{SM}}{{SQ \cdot SP}}\)
Mà \(SM = SP - MP = SP - MQ = SP - (SM - SQ) = SP + SQ - SM \Rightarrow SP + SQ = 2SM\)
Nên ta có: \(\frac{1}{{SK}} = \frac{{SM}}{{SQ \cdot SP}} \Leftrightarrow \frac{2}{{SK}} = \frac{{2SM}}{{SQ \cdot SP}} \Leftrightarrow \frac{2}{{SK}} = \frac{{SQ + SP}}{{SQ \cdot SP}} \Leftrightarrow \frac{2}{{SK}} = \frac{1}{{SQ}} + \frac{1}{{SP}}\).
Lời giải
Đánh số các ô của bảng như hình vẽ.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
8 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
7 |
8 |
1 |
2 |
3 |
4 |
5 |
6 |
|
6 |
7 |
8 |
1 |
2 |
3 |
4 |
5 |
|
5 |
6 |
7 |
8 |
1 |
2 |
5 |
4 |
|
4 |
5 |
6 |
7 |
8 |
1 |
2 |
3 |
|
3 |
4 |
5 |
6 |
7 |
8 |
1 |
2 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
1 |
Theo nguyên lí Dirichle đặt 33 quân cờ vào mỗi ô mà có 8 loại ô là các số được đánh từ 1 đến 8 nên có ít nhất 5 quân cờ cùng một số. Theo bảng này các quân cờ được đặt trong các ô có cùng số thì không chiếu nhau.
Suy ra điều phải chứng minh.
