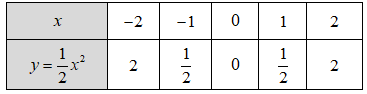Quảng cáo
Trả lời:
|
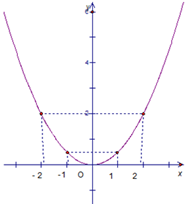
Ta có bảng giá trị của \(y\) tương ứng với giá trị của \(x\) như sau:
|
|
|
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
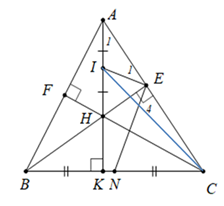
a) Chứng minh bốn điểm \(A\), \(E\), \(H\), .\(F\). nằm trên cùng một đường tròn. |
|
|
|
Ta có \[\widehat {AEB} = 90^\circ \] (do \(BE\) là đường cao của \(\Delta ABC\)) hay \[\widehat {AEH} = 90^\circ \]. |
|
\[\widehat {AFC} = 90^\circ \] (do \(CF\) là đường cao của \(\Delta ABC\)) hay \[\widehat {AFH} = 90^\circ \]. |
|
Suy ra bốn điểm \(A,E,H,F\) cùng nằm trên một đường tròn đường kính \(AH\) (đpcm) |
|
b) Chứng minh \(NE\) là tiếp tuyến của đường tròn đường kính \(AH\). |
|
Vì \(I\) là trung điểm của đoạn thẳng \(AH\) nên \(I\) là tâm đường tròn đường kính \(AH\) suy ra \(IA = IE\) Vì\(\Delta IAE\) cân tại \(I\) nên \({\widehat A_1} = {\widehat E_1}\) (1) |
|
\[\Delta EBC\] vuông tại \[E\]có \[EN\] là đường trung trrung tuyến ứng với cạnh huyền \[BC\] Nên \(EN = NC = \frac{{BC}}{2}\,\) Suy ra \[\Delta ENC\] cân tại \[N\] nên \(\widehat {NCE} = \widehat {{E_4}}\) (2) Xét \[\Delta AKC\] vuông tại \[K\] có \[\widehat {KCA} + {\widehat A_1} = 90^\circ \] hay \[\widehat {NCE} + {\widehat A_1} = 90^\circ \] (3) Từ (1), (2), (3) suy ra \({\widehat E_1} + {\widehat E_4} = 90^\circ \) |
|
Lại có \({\widehat E_1} + {\widehat E_4} + \widehat {IEN} = 180^\circ \) (do \(A;\;E;\;C\) thẳng hàng) Suy ra \(90^\circ + \widehat {IEN} = 180^\circ \) hay \(\widehat {IEN} = 90^\circ \) Suy ra \(EN \bot EI\) tại \(E\) Do đó \(NE\) là tiếp tuyến của đường tròn đường kính \(AH\) (đpcm) |
|
c) Chứng minh \(C{I^2} - I{E^2} = CK.CB\). |
|
Áp dụng định lí Pythagore \(\Delta CIK\) vuông tại \(K\), ta có: \(C{I^2} = C{K^2} + I{K^2}\) Lại có \(IA = IE = IH\) (cùng bán kính đường tròn tâm I) Suy ra \[C{I^2} - I{E^2} = C{K^2} + I{K^2} - I{E^2}\] \[C{I^2} - I{E^2} = C{K^2} + (IK + IE)(IK - IE)\] \[C{I^2} - I{E^2} = C{K^2} + (IK + IE)(IK - IH)\] \[ = C{K^2} + AK\;.\;KH\] \(\left( 4 \right)\) Ta lại có \[CK.CB = CK(CK + KB)\] \[ = C{K^2} + CK\;.\;KB\] \(\left( 5 \right)\) |
|
Xét \(\Delta KBH\) và \(\Delta KAC\) có \(\widehat {KBH} = \widehat {KAC}\) (\( = 90^\circ - \widehat {ACB}\)); \[\widehat {BKH} = \widehat {AKC} = 90^\circ \] Do đó \[\left( {g - g} \right)\] Nên \(\frac{{KB}}{{KA}} = \frac{{KH}}{{KC}}\) suy ra \(KA\;.\;KH = KB\;.\;KC\) hay \(AK\;.\;KH = CK\;.\;KB\) \(\left( 6 \right)\) Từ \[\left( 4 \right)\],\(\left( 5 \right)\) và \(\left( 6 \right)\) suy ra \[C{I^2} - I{E^2} = CK\;.\;CB\] (đpcm) |
Lời giải
|
a) Tính giá trị của biểu thức \[A\] tại \[x = 25\]. |
|
Tại \(x = 25\)(thỏa mãn điều kiện xác định) \[A = \frac{{\sqrt x - 2}}{{\sqrt x + 2}} = \frac{{\sqrt {25} - 2}}{{\sqrt {25} + 2}} = \frac{3}{7}\] |
|
Vậy \[A = \frac{3}{7}\] khi \[x = 25\] |
|
b) Chứng minh \[B = \frac{{\sqrt x - 1}}{{\sqrt x - 2}}\]. |
|
Với \[x \ge 0\], \[x \ne 4\]. Ta có : \(B = \frac{{\sqrt x + 2}}{{\sqrt x - 2}} - \frac{3}{{\sqrt x + 2}} - \frac{{12}}{{x - 4}}\) \(B = \frac{{{{\left( {\sqrt x + 2} \right)}^2}}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} - \frac{{3\left( {\sqrt x - 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} - \frac{{12}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\) \(B = \frac{{x + 4\sqrt x + 4 - 3\sqrt x + 6 - 12}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \frac{{x + \sqrt x - 2}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}}\) \(B = \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 2} \right)}}{{\left( {\sqrt x - 2} \right)\left( {\sqrt x + 2} \right)}} = \frac{{\sqrt x - 1}}{{\sqrt x - 2}}\) |
|
c) Với \[P = A.B\]. Tìm giá trị của \(x\) để \[\left| P \right| > P\]. |
|
Ta có : \[P = A.B = \frac{{\sqrt x - 2}}{{\sqrt x + 2}}.\frac{{\sqrt x - 1}}{{\sqrt x - 2}} = \frac{{\sqrt x - 1}}{{\sqrt x + 2}}\] Tìm giá trị của \(x\) để \[\left| P \right| > P\] TH 1: \[P > P\] (vô lí) TH 2: \( - P > P\) hay \(\frac{{1 - \sqrt x }}{{\sqrt x + 2}} > \frac{{\sqrt x - 1}}{{\sqrt x + 2}}\) \( \Rightarrow 1 - \sqrt x > \sqrt x - 1 \Leftrightarrow 2 > 2\sqrt x \) \( \Leftrightarrow 1 > \sqrt x \Leftrightarrow 1 > x\) Kết hợp với điều kiện xác định ta có: \[0 \le x < 1\] |
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.