Một tàu điện dừng lại ở một sân ga, có ba toa tàu mang số 1, 2, 3 mở cửa để đón khách. Hai bạn Hương và Giang mỗi người chọn ngẫu nhiên một toa để lên (không tính thứ tự lên trước, lên sau). Mô tả không gian mẫu của phép thử và tính xác suất của biến cố E: “Hương và Giang cùng đi lên một toa tàu”.

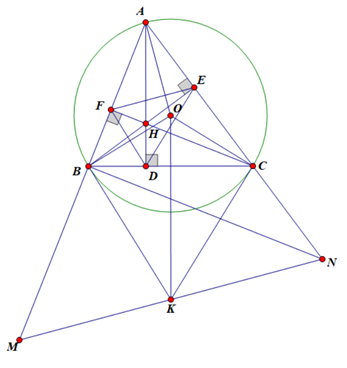
a)     Do AD, BE là các đường cao của \[\Delta ABC\]nên \[\Delta HDC\]vuông tại D

Do đó H, C, D cùng thuộc đường tròn đường kính HC.

Tương tự \[\Delta HEC\]vuông tại E nên H, C, E cùng thuộc đường tròn đường kính HC

Vậy H, E, C, D cùng thuộc đường tròn đường kính HC hay tứ giác CDHE nội tiếp đường tròn.

    b) Chứng minh tương tự câu a, ta có \[\Delta BEC\] vuông tại E và \[\Delta BFC\] vuông tại F nên B, C, E, F cùng thuộc đường tròn đường kính BC. Suy ra \[\widehat {EFC} = \widehat {EBC}\] (hai góc nội tiếp cùng chắn cung EC)

Do tứ giác EFCB nội tiếp nên \[\widehat {FEB} = \widehat {FCB}\] (hai góc nội tiếp cùng chắn cung FB)

Lại có \[\widehat {HED} = \widehat {HCD}\] (hai góc nội tiếp cùng chắn cung HD) nên \[\widehat {FEB} = \widehat {BED}\]

Kết hợp với \[\widehat {EFH} = \widehat {HBD}\] (hai góc nội tiếp cùng chắn cung CE) suy ra \[\Delta H{\rm{EF}} \sim \Delta {\rm{DEB(g}}{\rm{.g)}}\]

Suy ra \[\frac{{HE}}{{DE}} = \frac{{HF}}{{DB}}{\rm{ hay }}HE.{\rm{ }}DB{\rm{ }} = {\rm{ }}HF.{\rm{ }}DE\] (đpcm)

c) Ta có KB = KC (tính chất hai tiếp tuyến cắt nhau) và OB = OC (Cùng bằng bán kính của (O))

Suy ra OK là trung trực của đoạn thằng BC

Ta có: \[\widehat {OBK} = 90^\circ \] (do BK là tiếp tuyến) nên \[\widehat {MBK} + \widehat {OBA} = 180^\circ  - \widehat {OBK} = 90^\circ \]

Hay \[\widehat {MBK} = 90^\circ  - \widehat {OBA}{\rm{  (1)}}\]

Ta có \[\widehat {ACB} = \widehat {AFE}\] (do cùng cộng với \[\widehat {EFB}\] bằng \[180^\circ \]

Suy ra \[\widehat {OBA} = \widehat {OAB} = \frac{{180^\circ  - \widehat {AOB}}}{2} = 90^\circ  - \frac{{\widehat {AOB}}}{2} = 90^\circ  - \widehat {ACB} = 90^\circ  - \widehat {AFE}\]

Thay vào (1) suy ra \[\widehat {MBK} = 90^\circ  - \left( {90^\circ  - \widehat {AFE}} \right) = \widehat {AFE}\]

Mà \[\widehat {AFE} = \widehat {AMN}\] (vì là hai góc đồng vị) nên \[\widehat {MBK} = \widehat {BMK}\]hay \[\Delta MBK\]cân tại K

Suy ra MK = KB

Chứng minh tương tự ta được \[\Delta KCN\]cân tại K hay KC = KN

Vậy KM = KN = KB = KC hay M, N, C, B cùng thuộc một đường tròn đường kính MN

Suy ra \[\widehat {MBN} = 90^\circ \] (góc nội tiếp chắn nửa đường tròn)

Vậy \[AM \bot BN\]

                Xét phương trình \[{x^2} - 5x + 2 = 0\] có a = 1, b = -5, c =2

\[\Delta  = {( - 5)^2} - 4.1.2 = 17 > 0\] nên phương trình có 2 nghiệm phân biệt

Theo định lí Viète, ta có:

\[\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 5\\{x_1}.{x_2} = \frac{c}{a} = 2\end{array} \right.\]

           \[B = \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{{{x_1} + {x_2}}}{{{x_1}.{x_2}}} = \frac{5}{2}\].

Vậy \[B = \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}} = \frac{5}{2}\].