Giải hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{x - y = 1}\\{2x + y = 8}\end{array}} \right.\)
Quảng cáo
Trả lời:
Ta có \(\left\{ {\begin{array}{*{20}{c}}{x - y = 1}\\{2x + y = 8}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}{x - y = 1}\\{3x = 9}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}{x = 3}\\{y = x - 1}\end{array}} \right.\)
\(\left\{ {\begin{array}{*{20}{c}}{x = 3}\\{y = 2}\end{array}} \right.\)
Vậy hệ phương trình có nghiệm duy nhất là \(\left( {x,y} \right) = \left( {3;2} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có: \(\Delta = {\left( { - 5} \right)^2} - 4.2 = 17 > 0\)
Do đó phương trình (*) luôn có hai nghiệm phân biệt \({x_1},{x_2}\)
b) Theo định lí Viete ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} = 5\\{x_1}{x_2} = 2\end{array} \right.\)
Khi đó \(P = {x_1} + {x_2} + \frac{1}{{{x_1}}} + \frac{1}{{{x_2}}}\)
\( = {x_1} + \;{x_2} + \frac{{{x_1} + {x_2}}}{{{x_1}{x_2}}}\)
\( = 5 + \frac{5}{2} = \frac{{15}}{2}\)
Vậy \(P = \frac{{15}}{2}\).
Lời giải
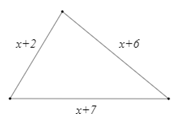
Chu vi hình tam giác là: \(\left( {x + 2} \right) + \left( {x + 6} \right) + \left( {x + 7} \right) = 3x + 15\)
Chu vi hình chữ nhật là: \(2\left( {x + 1 + x + 3} \right) = 2\left( {2x + 4} \right) = 4x + 8\)
Chu vi tam giác lớn hơn chu vi hình chữ nhật: \(3x + 15 > 4x + 8\)
\( - x > - 7\)
\(x < 7\)
Kết hợp với điều kiện \(x > 0\) ta được \(0 < x < 7\).
Vậy \(0 < x < 7\) là giá trị cần tìm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.