Thí sinh không được dùng máy tính, hãy giải phương trình bậc hai: \[3{x^2} - 5x + 2 = 0\]
Thí sinh không được dùng máy tính, hãy giải phương trình bậc hai: \[3{x^2} - 5x + 2 = 0\]
Quảng cáo
Trả lời:
Xét phương trình có \[a = 3,b = - 5,c = 2\].
\[ \to \Delta = {b^2} - 4ac = {\left( { - 5} \right)^2} - 4.3.2 = 1 > 0\]
Do đó, phương trình có hai nghiệm phân biệt:
\[{x_1} = \frac{{ - b + \sqrt \Delta }}{{2a}} = 1,{x_2} = \frac{{ - b - \sqrt \Delta }}{{2a}} = \frac{2}{3}\]
Vậy phương trình có hai nghiệm \[{x_1} = 1;{x_2} = \frac{2}{3}\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Ta có không gian mẫu là \[{n_\Omega } = 10\].
Ta có \[A = \{ \left( {1,3} \right);\left( {1,4} \right);\left( {1,5} \right);\left( {2,3} \right);\left( {2,4} \right);\left( {2,5} \right)\} \], suy ra \[n\left( A \right) = 6\].
Xác suất của biến cố \[A\] là \[P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{3}{5}\]
Lời giải
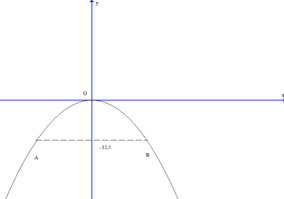
Giả sử \[A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\]
Vì \[A\] thuộc đồ thị của hàm số \[y = - \frac{1}{2}{x^2}\] nên \[A\left( {{x_A}; - \frac{1}{2}{x_A}^2} \right)\].
Vì tung độ của điểm \[A\] bằng \[ - 12,5\] nên \[ - \frac{1}{2}{x_A}^2 = - 12,5 \to {x_A}^2 = 25\]
Vì điểm \[A\] có hoành độ dương nên \[{x_A} = 5 \to A\left( {5; - 12,5} \right)\]
Tương tự, ta có: \[B\left( { - 5; - 12,5} \right)\]
Vì \[A,B\] có cùng tung độ nên đoạn thẳng \[AB\] song song với trục \[Ox\].
Do đó: \[AB = \left| {{x_A}} \right| + \left| {{x_B}} \right| = 5 + 5 = 10\]
Vậy chiều rộng của cổng là \[10\] \[m\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.