Cho hình thang ABCD (AD song song với BC, AD < BC). Các điểm E, F lần lượt thuộc các cạnh AB, CD. Đường tròn ngoại tiếp tam giác AEF cắt đường thẳng AD tại M (M không trùng với A và D, D nằm giữa A và M), đường tròn ngoại tiếp tam giác CEF cắt đường thẳng BC tại điểm N (N không trùng với B và C, B nằm giữa C và N). Đường thẳng AB cắt đường thẳng CD tại điểm P, đường thẳng EN cắt đường thẳng FM tại điểm Q. Chứng minh rằng:
a) Tứ giác EFQP nội tiếp đường tròn.
b) PQ song song với BC và tâm đường tròn ngoại tiếp các tam giác PQE, AMF, CEN cùng nằm trên một đường thẳng cố định.
c) Các đường thẳng MN, BD, EF đồng quy tại một điểm.
Cho hình thang ABCD (AD song song với BC, AD < BC). Các điểm E, F lần lượt thuộc các cạnh AB, CD. Đường tròn ngoại tiếp tam giác AEF cắt đường thẳng AD tại M (M không trùng với A và D, D nằm giữa A và M), đường tròn ngoại tiếp tam giác CEF cắt đường thẳng BC tại điểm N (N không trùng với B và C, B nằm giữa C và N). Đường thẳng AB cắt đường thẳng CD tại điểm P, đường thẳng EN cắt đường thẳng FM tại điểm Q. Chứng minh rằng:
a) Tứ giác EFQP nội tiếp đường tròn.
b) PQ song song với BC và tâm đường tròn ngoại tiếp các tam giác PQE, AMF, CEN cùng nằm trên một đường thẳng cố định.
c) Các đường thẳng MN, BD, EF đồng quy tại một điểm.
Quảng cáo
Trả lời:
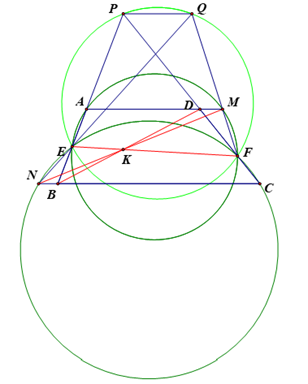
a) Ta có:
\[\widehat {EQF} = \widehat {{\rm{NEF}}} - \widehat {QF{\rm{E}}} = \left( {180^\circ - \widehat {FCN}} \right) - \widehat {PA{\rm{D}}}\]
Vì AD // BC nên \[\widehat {FCN} = \widehat {PDA}\] (2 góc đồng vị)
Do đó: \[\widehat {EQF} = 180^\circ - \widehat {P{\rm{D}}A} - \widehat {PA{\rm{D}}} = \widehat {EPF}\]
Suy ra tứ giác EFQP nội tiếp đường tròn.
b) Vì tứ giác EFQP nội tiếp nên \[\widehat {QPA} = 180^\circ - \widehat {QF{\rm{E}}} = 180^\circ - \widehat {PA{\rm{D}}}\]
\[ \Rightarrow \widehat {QPA} + \widehat {PA{\rm{D}}} = 180^\circ \].
Mà hai góc ở vị trí trong cùng phía \[ \Rightarrow \] PQ // AD
Gọi \[\left( {{O_1}} \right);\left( {{O_2}} \right);\left( {{O_3}} \right)\] lần lượt là các đường tròn ngoại tiếp tam giác PQE; AM; CEN
Do \[\left( {{O_1}} \right)\] cắt \[\left( {{O_2}} \right)\] tại E và F nên \[{O_1}{O_2} \bot EF\,\,\,\,\,\,(1)\]
Do \[\left( {{O_2}} \right)\] cắt \[\left( {{O_3}} \right)\] tại E và F nên \[{O_2}{O_3} \bot EF\,\,\,\,\,\,(2)\]
Từ (1) và (2) suy ra \[{O_1};{O_2};{O_3}\] thẳng hàng (đpcm)
c) Giả sử MN cắt EF tại K. Ta chứng minh B, D, K thẳng hàng.
Áp dụng định lý Menelaus cho tam giác MNQ và cát tuyến KEF ta được:
\[\frac{{KM}}{{KN}}.\frac{{EN}}{{EQ}}.\frac{{FQ}}{{FM}} = 1\]
Suy ra \[\frac{{KM}}{{KN}} = \frac{{EQ}}{{EN}}.\frac{{FM}}{{FQ}} = \frac{{PQ}}{{NB}}.\frac{{DM}}{{PQ}} = \frac{{DM}}{{NB}}\].
Kết hợp với MD // NB, suy ra B, D, K thẳng hàng (đpcm).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Vì \[{x^2} + {y^2} + {z^2} = 2xyz\] nên \[2xyz\] chẵn, nên tồn tại ít nhất 1 số chẵn, giả sử là x chẵn.
Khi đó: \[{x^2} \vdots 4;\,\,\,\,2{\rm{x}}yz \vdots 4 \Rightarrow {y^2} + {z^2} \vdots 4\] (*)
Nếu y lẻ \[ \Rightarrow \] \[{y^2}\] lẻ \[ \Rightarrow \] lẻ \[{z^2}\]\[ \Rightarrow \] \[z\] lẻ
\[ \Rightarrow \left\{ \begin{array}{l}y = 2k + 1 \Rightarrow {y^2} = 4{k^2} + 4k + 1\\z = 2m + 1 \Rightarrow {z^2} = 4{m^2} + 4m + 1\end{array} \right.\,\,\,\,\,\,\,\,\left( {k;m \in Z} \right)\]
\[ \Rightarrow {y^2} + {z^2} = 4{k^2} + 4k + 4{m^2} + 4m + 2\]
\[ \Rightarrow {y^2} + {z^2}\] chia 4 dư 2 (không thỏa mãn(*))
Do đó y chẵn và z chẵn \[ \Rightarrow y \vdots 2;\,\,\,z \vdots 2\]
\[ \Rightarrow xyz \vdots 8\,\,\,(1)\]
Giả sử cả 3 số x, y, z đều không chia hết cho 3 vì x; y; z chẵn nên \[{x^2};{y^2};{z^2} \equiv 1(mo{\rm{d}}\,{\rm{3)}}\]
\[ \Rightarrow {x^2} + {y^2} + {z^2} \vdots 3\]
Do đó \[2xyz \vdots 3 \Rightarrow xyz \vdots 3\] (mâu thuẫn với giả thiết x, y, z đều không chia hết cho 3)
Nên tồn tại 1 số chia hết cho 3 hay \[xyz \vdots 3\,\,\,\,\,\,\,\,\,(2)\]
Từ (1) và (2) suy ra: \[xyz \vdots 24\]
Vậy \[xyz \vdots 24\].
b) Đặt \[A = {\left( {a + b + c} \right)^2} - 2a + 2b\]
Ta có:
\[\begin{array}{l}{\left( {a + b + c + 1} \right)^2} = {\left( {a + b + c} \right)^2} + 2\left( {a + b + c} \right) + 1 > A\\{\left( {a + b + c - 1} \right)^2} = {\left( {a + b + c} \right)^2} - 2\left( {a + b + c} \right) + 1 < A\end{array}\]
Nên \[{\left( {a + b + c - 1} \right)^2} < A < {\left( {a + b + c + 1} \right)^2}\]
Mà A chính phương nên \[A = {\left( {a + b + c} \right)^2}\]
\[ \Rightarrow {\left( {a + b + c} \right)^2} - 2{\rm{a}} + 2b = {\left( {a + b + c} \right)^2}\]
\[ \Leftrightarrow 2{\rm{a}} = 2b \Leftrightarrow a = b\]
Vậy tất cả các bộ (a; b; c) cần tìm là (k; k; m) với k, m nguyên dương bất kì.
Lời giải
a) Giải phương trình \[4{x^2} - x - 3 = 2\sqrt {x + 2} \] (ĐKXĐ: \[x \ge - 2\])
Bình phương hai vế của phương trình ta được:
\[\begin{array}{l}{\left( {4{x^2} - x - 3} \right)^2} = 4\left( {x + 2} \right)\\ \Leftrightarrow 16{x^4} + {x^2} + 9 - 8{x^3} + 6x - 24{x^2} = 4x + 8\\ \Leftrightarrow 16{x^4} - 8{x^3} - 23{x^2} + 2x + 1 = 0\\ \Leftrightarrow \left( {16{x^4} + 16{x^3}} \right) - \left( {24{x^3} + 24{x^2}} \right) + \left( {{x^2} + 2x + 1} \right) = 0\\ \Leftrightarrow 16{x^3}\left( {x + 1} \right) - 24{x^2}\left( {x + 1} \right) + \left( {x + {1^2}} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {16{x^3} - 24{x^2} + x + 1} \right) = 0\\ \Leftrightarrow \left( {x + 1} \right)\left[ {\left( {16{x^3} - 4{x^2}} \right) - \left( {20{x^2} - 5x} \right) - \left( {4x - 1} \right)} \right] = 0\\ \Leftrightarrow \left( {x + 1} \right)\left[ {4{x^2}\left( {4x - 1} \right) - 5x\left( {4x - 1} \right) - \left( {4x - 1} \right)} \right] = 0\\ \Leftrightarrow \left( {x + 1} \right)\left( {4x - 1} \right)\left( {4{x^2} - 5x - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 1 = 0\\4x - 1 = 0\\4{x^2} - 5x - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = \frac{1}{4}\\4{x^2} - 5x - 1 = 0\,\,\,\,\,(*)\end{array} \right.\end{array}\]
Giải (*):\[\Delta = {\left( { - 5} \right)^2} - 4.4.\left( { - 1} \right) = 41\]
Phương trình (*) có hai nghiệm phân biệt: \[\left[ \begin{array}{l}x = \frac{{5 + \sqrt {41} }}{8}\\x = \frac{{5 - \sqrt {41} }}{8}\end{array} \right.\]
Thử lại vào phương trình đã cho ta được tập nghiệm của phương trình là: \[S = \left\{ { - 1;\frac{{5 + \sqrt {41} }}{8}} \right\}\].
b) Giải phương trình: \[{x^2} + \frac{{4{x^2}}}{{{{\left( {x + 2} \right)}^2}}} = 5\] (ĐKXĐ: \[x \ne - 2\])
\[ \Leftrightarrow \]\[{x^2} - \frac{{4{x^2}}}{{x + 2}} + \frac{{4{x^2}}}{{{{(x + 2)}^2}}} + \frac{{4{x^2}}}{{x + 2}} - 5 = 0\]
\[ \Leftrightarrow {\left( {x - \frac{{2x}}{{x + 2}}} \right)^2} + \frac{{4{x^2}}}{{x + 2}} - 5 = 0\]
\[ \Leftrightarrow {\left( {\frac{{{x^2}}}{{x + 2}}} \right)^2} + \frac{{4{x^2}}}{{x + 2}} - 5 = 0\,\,\,\,\,\,(1)\]
Đặt \[t = \frac{{{x^2}}}{{x + 2}}\], phương trình (1) trở thành: \[{t^2} + 4t - 5 = 0\,\,\,\,\,\,\,(2)\]
Vì \[1 + 4 + ( - 5) = 0\] nên phương trình (2) có 2 nghiệm \[{t_1} = 1;\,\,{t_2} = - 5\]
Với \[{t_1} = 1\] ta có:
\[\frac{{{x^2}}}{{x + 2}} = 1 \Leftrightarrow {x^2} = x + 2 \Leftrightarrow {x^2} - x - 2 = 0\,\,\,\,\,(3)\]
Vì \[1 - ( - 1) + ( - 2) = 0\] nên phương trình (3) có 2 nghiệm \[{x_1} = - 1\,\,(tm);\,\,{x_2} = 2\,\,(tm)\]
Với \[{t_2} = - 5\] ta có:
\[\frac{{{x^2}}}{{x + 2}} = - 5 \Leftrightarrow {x^2} + 5{\rm{x}} + 10 = 0\] (Vô lí vì \[{x^2} + 5x + 10 = {\left( {x + \frac{5}{2}} \right)^2} + \frac{{15}}{4} > 0\,\,\,\,\forall x \in R\])
Vậy tập nghiệm của phương trình đã cho là: \[S = \left\{ { - 1;2} \right\}\]
c) Giải hệ phương trình: \[\left\{ \begin{array}{l}{{\rm{x}}^2} + {y^2} + x + y = 8\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\\2{x^2} + {y^2} - 3xy + 3x - 2y + 1 = 0\,\,\,\,\,\,\,\,\,(2)\end{array} \right.\]
Ta có: \[(2) \Leftrightarrow (2{x^2} - 2xy) - (xy - {y^2}) + (x - y) + (2x - y) + 1 = 0\]
\[\begin{array}{l} \Leftrightarrow 2x(x - y) - y(x - y) + (x - y) + (2x - y) + 1 = 0\\ \Leftrightarrow (x - y)(2x - y) + (x - y) + (2x - y + 1) = 0\\ \Leftrightarrow (x - y)(2x - y + 1) + (2x - y + 1) = 0\\ \Leftrightarrow (2x - y + 1)(x - y + 1) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2x - y + 1 = 0\\x - y + 1 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}y = 2x + 1\\y = x + 1\end{array} \right.\end{array}\]
Thay \[y = 2x + 1\] vào (1) ta được:
\[{x^2} + {\left( {2{\rm{x}} + 1} \right)^2} + x + 2x + 1 = 8 \Leftrightarrow 5{x^2} + 7x - 6 = 0\,\,\,\,\,\,\,\,(3)\]
\[\Delta = {7^2} - 4.5.\left( { - 6} \right) = 169\]
Phương trình (3) có 2 nghiệm phân biệt \[\left[ \begin{array}{l}x = \frac{{ - 7 + \sqrt {169} }}{{2.5}} = \frac{3}{5}\\x = \frac{{ - 7 - \sqrt {169} }}{{2.5}} = - 2\end{array} \right.\]
Với \[x = \frac{3}{5} \Rightarrow y = 2.\frac{3}{5} + 1 = \frac{{11}}{5}\]
Với \[x = - 2 \Rightarrow y = 2.\left( { - 2} \right) + 1 = - 3\]
Thay \[y = x + 1\] vào (1) ta được: \[{x^2} + {\left( {x + 1} \right)^2} + x + x + 1 = 8\] \[ \Leftrightarrow 2{x^2} + 4x - 6 = 0\,\,\,\,(4)\]
Vì \[2 + 4 + \left( { - 6} \right) = 0\]nên phương trình (4) có 2 nghiệm phân biệt: \[x = 1;x = - 3\]
Với \[x = 1 \Rightarrow y = 2\]
Với \[x = - 3 \Rightarrow y = - 2\]
Vậy nghiệm của hệ phương trình đã cho là: \[\left( {x;y} \right) \in \left\{ {\left( {\frac{3}{5};\frac{{11}}{5}} \right);\left( { - 2; - 3} \right);\left( {1;2} \right);\left( { - 3; - 2} \right)} \right\}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.