a) Rút gọn biểu thức \(A = \frac{{8 + x\left( {1 + \sqrt {x - 2\sqrt x  + 1} } \right)}}{{\left( {x - 4} \right)\left( {x - 2\sqrt x  + 4} \right)}} + \frac{{x - 3\sqrt x }}{{2\left( {x - \sqrt x  - 6} \right)}}\) (với \(x > 1,x \ne 4,x \ne 9\)).

b) Tìm tất cả bộ ba số nguyên tố \(p,q,r\)thỏa mãn \(pq = r + 1\) và \(2\left( {{p^2} + {q^2}} \right) = {r^2} + 1\).

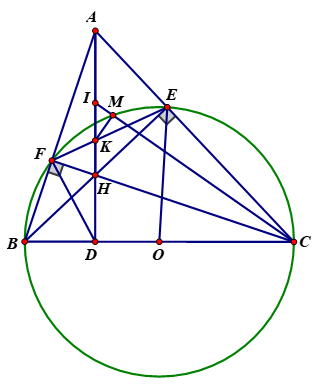
a) Ta có \(\widehat {BFC} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)

 \(\widehat {BEC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Xét tam giác ABC có: BE và CF là 2 đường cao cắt nhau tại H \( \Rightarrow \)H là trực tâm tam giác ABC \( \Rightarrow AH \bot BC\)tại D.

Ta có tứ giác BCEF nội tiếp (O) \( \Rightarrow \widehat {AFE} = \widehat {OCE}\)(góc ngoài bằng góc đối trong).

Xét tứ giác ACDF có:

\(\widehat {ADC} = 90^\circ \)(cmt)

\(\widehat {AFC} = 90^\circ \)(cmt)

\( \Rightarrow \)tứ giác ACDF nội tiếp \( \Rightarrow \widehat {BFD} = \widehat {OCE}\)(góc ngoài bằng góc đối trong).

Xét tam giác BEC vuông tại E có EO là trung tuyến

\( \Rightarrow EO = \frac{1}{2}BC = CO = BO\)(định lý đường trung tuyến của tam giác vuông)

\( \Rightarrow \widehat {OCE} = \widehat {OEC} \Rightarrow \widehat {COE} = 180^\circ - 2\widehat {OCE}\)

Ta có \[\left\{ \begin{array}{l}\widehat {AFE} = \widehat {OCE}\left( {cmt} \right)\\\widehat {BFD} = \widehat {OCE}\left( {cmt} \right)\end{array} \right.\]\( \Rightarrow \widehat {COE} = 180^\circ - \widehat {AFE} - \widehat {BFD} = \widehat {EFD}\)

Xét tứ giác ODFE có \[\widehat {COE} = \widehat {EFD}\left( {cmt} \right)\]

Mà hai góc ở vị trí góc ngoài và góc đối trong \( \Rightarrow \)tứ giác ODFE nội tiếp.

b) Xét tam giác AEH vuông tại E có EI là trung tuyến

\( \Rightarrow EI = \frac{1}{2}AH = AI = HI\)(định lý đường trung tuyến của tam giác vuông)

\( \Rightarrow \widehat {IAE} = \widehat {IEA}\), có \(\widehat {OCE} = \widehat {OEC}\left( {cmt} \right)\)và \(\widehat {IAE}\)phụ \(\widehat {OCE}\)\( \Rightarrow \widehat {IEA}\) phụ \(\widehat {OEC}\)\( \Rightarrow \widehat {OEI} = 90^\circ \)

Chứng minh tương tự ta có \(\widehat {OFI} = 90^\circ \).

Xét tứ giác OEIF có \[\widehat {OEI} + \widehat {OFI} = 180^\circ \]

Mà hai góc ở vị trí đối nhau \( \Rightarrow \)tứ giác OEIF nội tiếp.

Ta có tứ giác ODFE nội tiếp (cmt), tứ giác OEIF nội tiếp (cmt) \[ \Rightarrow \] 5 điểm O, D, F, I, E cùng thuộc đường tròn đường kính ID.

Xét \(\Delta IEK\)và \[\Delta IDE\]có:

\( \Rightarrow \frac{{IE}}{{ID}} = \frac{{IK}}{{IE}} \Leftrightarrow I{E^2} = ID.IK\left( 1 \right)\)

Xét \(\Delta IEM\)và \[\Delta ICE\]có:

\( \Rightarrow \frac{{IE}}{{IC}} = \frac{{IM}}{{IE}} \Leftrightarrow I{E^2} = IC.IM\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow IK.ID = IC.IM \Rightarrow \frac{{IK}}{{IM}} = \frac{{IC}}{{ID}}\)

Xét \(\Delta IMK\)và \[\Delta IDC\]có:

   mà \(\widehat {IDC} = 90^\circ \Rightarrow \widehat {IMK} = 90^\circ \Rightarrow CI \bot KM\).

Theo đề ta có: \(\frac{1}{x} + \frac{1}{y} + \frac{1}{z} = 1\)

Đặt \(\frac{1}{x} = a\), \(\frac{1}{y} = b\), \(\frac{1}{z} = c\)\(\left( {a,b,c > 0} \right)\)\( \Rightarrow a + b + c = 1\)

Khi đó \[H = \frac{c}{{9{a^2} + 1}} + \frac{a}{{9{b^2} + 1}} + \frac{b}{{9{c^2} + 1}}\]

Ta có: \[\frac{c}{{9{a^2} + 1}} \le \frac{{c\left( {9{a^2} + 1} \right) - 9{a^2}c}}{{9{a^2} + 1}} = c - \frac{{9{a^2}c}}{{9{a^2} + 1}}\]

Vì \[9{a^2} + 1 \ge 6a \Rightarrow c - \frac{{9{a^2}c}}{{9{a^2} + 1}} \ge c - \frac{{9{a^2}c}}{{6a}} = c - \frac{3}{2}ac\]

Chứng minh tương tự ta có: \[\frac{a}{{9{b^2} + 1}} \ge a - \frac{3}{2}ba\]; \[\frac{b}{{9{c^2} + 1}} \ge b - \frac{3}{2}cb\]

\[ \Rightarrow H \ge a + b + c - \frac{3}{2}\left( {ab + bc + ca} \right)\]

Mà \[ab + bc + ca \le \frac{{{{\left( {a + b + c} \right)}^2}}}{3}\]

\[ \Rightarrow H \ge 1 - \frac{3}{2}.\frac{1}{3} = \frac{1}{2}\]

Vậy \[{H_{\min }} = \frac{1}{2}\]. Dấu bằng xảy ra khi và chỉ khi \[x = y = z = 3\].