Đề thi tuyển sinh vào lớp 10 môn Toán chuyên năm 2021-2022 sở GD&ĐT Quảng Nam có đáp án

a) Rút gọn biểu thức \(A = \frac{{8 + x\left( {1 + \sqrt {x - 2\sqrt x  + 1} } \right)}}{{\left( {x - 4} \right)\left( {x - 2\sqrt x  + 4} \right)}} + \frac{{x - 3\sqrt x }}{{2\left( {x - \sqrt x  - 6} \right)}}\) (với \(x > 1,x \ne 4,x \ne 9\))

Với \(x > 1,x \ne 4,x \ne 9\)ta có:

\[\begin{array}{l}A = \frac{{8 + x\left( {1 + \sqrt {x - 2\sqrt x  + 1} } \right)}}{{\left( {x - 4} \right)\left( {x - 2\sqrt x  + 4} \right)}} + \frac{{x - 3\sqrt x }}{{2\left( {x - \sqrt x  - 6} \right)}}\\\,\,\,\,\, = \frac{{8 + x\left( {1 + \sqrt {{{\left( {\sqrt x  - 1} \right)}^2}} } \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)\left( {x - 2\sqrt x  + 4} \right)}} + \frac{{\sqrt x \left( {\sqrt x  - 3} \right)}}{{2\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 2} \right)}}\\\,\,\,\,\, = \frac{{8 + x\left( {1 + \left| {\sqrt x  - 1} \right|} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {x\sqrt x  + 8} \right)}} + \frac{{\sqrt x \left( {\sqrt x  - 3} \right)}}{{2\left( {\sqrt x  - 3} \right)\left( {\sqrt x  + 2} \right)}}\\\,\,\,\,\, = \frac{{8 + x\sqrt x }}{{\left( {\sqrt x  - 2} \right)\left( {x\sqrt x  + 8} \right)}} + \frac{{\sqrt x }}{{2\left( {\sqrt x  + 2} \right)}}\\\,\,\,\,\, = \frac{1}{{\left( {\sqrt x  - 2} \right)}} + \frac{{\sqrt x }}{{2\left( {\sqrt x  + 2} \right)}}\\\,\,\,\,\, = \frac{{2\left( {\sqrt x  + 2} \right) + \sqrt x \left( {\sqrt x  - 2} \right)}}{{2\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\\,\,\,\,\, = \frac{{x + 4}}{{2\left( {x - 4} \right)}}\end{array}\]

b) Tìm tất cả bộ ba số nguyên tố \(p,q,r\)thỏa mãn \(pq = r + 1\) và \(2\left( {{p^2} + {q^2}} \right) = {r^2} + 1\).

Đặt \(\left\{ \begin{array}{l}S = p + q\\P = p.q\end{array} \right.\)ta có hệ:

\(\left\{ \begin{array}{l}P = r + 1\\2\left( {{S^2} - 2P} \right) = {r^2} + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}P = r + 1\\2\left( {{S^2} - 2P} \right) = {r^2} + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}P = r + 1\\{S^2} = \frac{{{r^2} + 4r + 5}}{2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}P = r + 1\\S = \sqrt {\frac{{{r^2} + 4r + 5}}{2}} \end{array} \right.\)

Vì \(p,q,r\) là ba số nguyên tố nên ta có:

\(\left\{ \begin{array}{l}r = 5\\S = 5\\P = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}r = 5\\p + q = 5\\p.q = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}r = 5\\q = 5 - p\\p.\left( {5 - p} \right) = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}r = 5\\q = 5 - p\\{p^2} - 5p + 6 = 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}r = 5\\p = 2\\q = 3\end{array} \right.\)hoặc \(\left\{ \begin{array}{l}r = 5\\p = 3\\q = 2\end{array} \right.\).

Phương trình hoành độ giao điểm của (P) và (d):

\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} = \left( {2 - 2m} \right)x + m\\ \Leftrightarrow {x^2} - \left( {2 - 2m} \right)x - m = 0\,\,\left( 1 \right)\\\Delta  = {\left( {2 - 2m} \right)^2} - 4.1.\left( { - m} \right) = 4{m^2} - 4m + 4 = {\left( {2m + 1} \right)^2} + 3 > 0\,\,\forall m\end{array}\)

Do đó phương trình (1) luôn có hai nghiệm phân biệt với mọi m nên (d) luôn cắt (P) tại hai điểm phân biệt A, B với mọi giá trị của m.

Với mọi m, theo định lý Vi-et ta có:

\(\left\{ \begin{array}{l}{x_1} + {x_2} = \frac{{ - b}}{a} = 2 - 2m\\{x_1}.{x_2} = \frac{c}{a} =  - m\end{array} \right.\)

Vì  \(M\left( {\frac{1}{2};1} \right)\) là trung điểm của đoạn thẳng AB nên \(\frac{{{x_1} + {x_2}}}{2} = \frac{{2 - 2m}}{2} = \frac{1}{2} \Leftrightarrow m = \frac{1}{2}\)

Thay \(m = \frac{1}{2}\) vào (1) ta có phương trình: \({x^2} - x - \frac{1}{2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{{1 + \sqrt 3 }}{2} \Rightarrow y = \frac{{2 + \sqrt 3 }}{2}\\x = \frac{{1 - \sqrt 3 }}{2} \Rightarrow y = \frac{{2 - \sqrt 3 }}{2}\end{array} \right.\)

\( \Rightarrow A\left( {\frac{{1 + \sqrt 3 }}{2};\frac{{2 + \sqrt 3 }}{2}} \right),B\left( {\frac{{1 - \sqrt 3 }}{2};\frac{{2 - \sqrt 3 }}{2}} \right)\)

Vì H, K là hình chiếu của A, B lên trục hoành nên \( \Rightarrow H\left( {\frac{{1 + \sqrt 3 }}{2};0} \right),K\left( {\frac{{1 - \sqrt 3 }}{2};0} \right)\)

\( \Rightarrow HK = \left| {\frac{{1 + \sqrt 3 }}{2} - \frac{{1 - \sqrt 3 }}{2}} \right| = \sqrt 3 \).

a) Giải phương trình      \(\left( {x - 1} \right)\sqrt {7 - 2x}  = {x^2} - 3x + 2\). Điều kiện: \(x \le \frac{7}{2}\)

\( \Leftrightarrow \left( {x - 1} \right)\sqrt {7 - 2x}  = \left( {x - 1} \right)\left( {x - 2} \right)\)

\( \Leftrightarrow \left( {x - 1} \right)\sqrt {7 - 2x}  - \left( {x - 1} \right)\left( {x - 2} \right) = 0\)

\( \Leftrightarrow \left( {x - 1} \right)\left( {\sqrt {7 - 2x}  - x + 2} \right) = 0\)

\[ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\\sqrt {7 - 2x}  = x - 2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\\left\{ \begin{array}{l}x \ge 2\\7 - 2x = {\left( {x - 2} \right)^2}\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\\left\{ \begin{array}{l}x \ge 2\\ - {x^2} + 2x + 3 = 0\end{array} \right.\end{array} \right.\]

\[ \Leftrightarrow \left[ \begin{array}{l}x = 1\\\left\{ \begin{array}{l}x \ge 2\\\left[ \begin{array}{l}x = 3\\x =  - 1\end{array} \right.\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.\]

Vậy tập nghiệm của phương trình: \(S = \left\{ {1;3} \right\}\).

b) Giải hệ phương trình \(\left\{ \begin{array}{l}x + 2y - xy - 2 = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\\{x^2} - {y^2} + 2{x^2}y + 2x{y^2} + 1 = 0\left( 2 \right)\end{array} \right.\)

Giải (1) ta có:      \(x + 2y - xy - 2 = 0\)

                    \( \Leftrightarrow x\left( {1 - y} \right) - 2\left( {1 - y} \right) = 0\)

                    \( \Leftrightarrow x\left( {1 - y} \right) - 2\left( {1 - y} \right) = 0\)

                    \( \Leftrightarrow \left( {1 - y} \right)\left( {x - 2} \right) = 0\)

                    \( \Leftrightarrow \left[ \begin{array}{l}x = 2\\y = 1\end{array} \right.\)

Với x = 2 thay vào phương trình (2) ta có:

                         \(4 - {y^2} + 8y + 4{y^2} + 1 = 0\)

                    \( \Leftrightarrow 3{y^2} + 8y + 5 = 0\)

                    \( \Leftrightarrow \left[ \begin{array}{l}y =  - 1\\y = \frac{{ - 5}}{3}\end{array} \right.\)

Với y = 1 thay vào phương trình (2) ta có:

                    \({x^2} - 1 + 2{x^2} + 2x + 1 = 0 \Leftrightarrow 3{x^2} + 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \frac{{ - 2}}{3}\end{array} \right.\)

Vậy nghiệm của hệ phương trình là: \(\left( {x;y} \right) \in \left\{ {\left( {2; - 1} \right);\left( {2;\frac{{ - 5}}{3}} \right);\left( {0;1} \right);\left( {\frac{{ - 2}}{3};1} \right)} \right\}\).

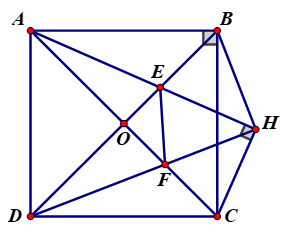
a) Ta có \(\widehat {ADC} = 90^\circ \)(ABCD là hình vuông)

    \(\widehat {AHC} = 90^\circ \) (H là hình chiếu của C trên AE)

Xét tứ giác ADCH có: \(\widehat {ADC} + \widehat {AHC} = 180^\circ \)

Mà hai góc này ở vị trí đối nhau

\( \Rightarrow \) Tứ giác ADCH nội tiếp.

\( \Rightarrow \widehat {DAC} = \widehat {DHC} = 45^\circ \)(cùng chắn cung CD) mà \(\widehat {AHD} + \widehat {DHC} = 90^\circ \)\( \Rightarrow \)\(\widehat {AHD} = 45^\circ \)

\( \Rightarrow \) HD là tia phân giác của góc AHC.

b) Xét tứ giác OEHC có: \(\widehat {EOC} + \widehat {EHC} = 180^\circ \).

Mà hai góc này ở vị trí đối nhau

\( \Rightarrow \)Tứ giác OEHC nội tiếp.

\( \Rightarrow \widehat {AEO} = \widehat {ACH}\)(góc ngoài bằng góc đối trong)                                                       (1) 

Tứ giác ADCH nội tiếp (cmt) \( \Rightarrow \widehat {ADF} = \widehat {ACH}\)(cùng chắn cung AH)                       (2)

Từ (1) và (2) suy ra \( \Rightarrow \widehat {AED} = \widehat {ADF}\)

Xét \(\Delta ADE\)và \(\Delta FAD\)có:\(\)\(\)

\( \Rightarrow \frac{{AF}}{{AD}} = \frac{{AD}}{{DE}} \Leftrightarrow AF.DE = A{D^2}\)

Ta có: \({S_{AEFD}} = \frac{1}{2}AF.DE = \frac{1}{2}A{D^2} = \frac{1}{2}{S_{ABCD}}\).

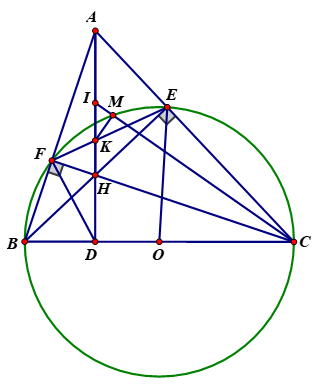
a) Ta có \(\widehat {BFC} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)

 \(\widehat {BEC} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn)

Xét tam giác ABC có: BE và CF là 2 đường cao cắt nhau tại H \( \Rightarrow \)H là trực tâm tam giác ABC \( \Rightarrow AH \bot BC\)tại D.

Ta có tứ giác BCEF nội tiếp (O) \( \Rightarrow \widehat {AFE} = \widehat {OCE}\)(góc ngoài bằng góc đối trong).

Xét tứ giác ACDF có:

\(\widehat {ADC} = 90^\circ \)(cmt)

\(\widehat {AFC} = 90^\circ \)(cmt)

\( \Rightarrow \)tứ giác ACDF nội tiếp \( \Rightarrow \widehat {BFD} = \widehat {OCE}\)(góc ngoài bằng góc đối trong).

Xét tam giác BEC vuông tại E có EO là trung tuyến

\( \Rightarrow EO = \frac{1}{2}BC = CO = BO\)(định lý đường trung tuyến của tam giác vuông)

\( \Rightarrow \widehat {OCE} = \widehat {OEC} \Rightarrow \widehat {COE} = 180^\circ - 2\widehat {OCE}\)

Ta có \[\left\{ \begin{array}{l}\widehat {AFE} = \widehat {OCE}\left( {cmt} \right)\\\widehat {BFD} = \widehat {OCE}\left( {cmt} \right)\end{array} \right.\]\( \Rightarrow \widehat {COE} = 180^\circ - \widehat {AFE} - \widehat {BFD} = \widehat {EFD}\)

Xét tứ giác ODFE có \[\widehat {COE} = \widehat {EFD}\left( {cmt} \right)\]

Mà hai góc ở vị trí góc ngoài và góc đối trong \( \Rightarrow \)tứ giác ODFE nội tiếp.

b) Xét tam giác AEH vuông tại E có EI là trung tuyến

\( \Rightarrow EI = \frac{1}{2}AH = AI = HI\)(định lý đường trung tuyến của tam giác vuông)

\( \Rightarrow \widehat {IAE} = \widehat {IEA}\), có \(\widehat {OCE} = \widehat {OEC}\left( {cmt} \right)\)và \(\widehat {IAE}\)phụ \(\widehat {OCE}\)\( \Rightarrow \widehat {IEA}\) phụ \(\widehat {OEC}\)\( \Rightarrow \widehat {OEI} = 90^\circ \)

Chứng minh tương tự ta có \(\widehat {OFI} = 90^\circ \).

Xét tứ giác OEIF có \[\widehat {OEI} + \widehat {OFI} = 180^\circ \]

Mà hai góc ở vị trí đối nhau \( \Rightarrow \)tứ giác OEIF nội tiếp.

Ta có tứ giác ODFE nội tiếp (cmt), tứ giác OEIF nội tiếp (cmt) \[ \Rightarrow \] 5 điểm O, D, F, I, E cùng thuộc đường tròn đường kính ID.

Xét \(\Delta IEK\)và \[\Delta IDE\]có:

\( \Rightarrow \frac{{IE}}{{ID}} = \frac{{IK}}{{IE}} \Leftrightarrow I{E^2} = ID.IK\left( 1 \right)\)

Xét \(\Delta IEM\)và \[\Delta ICE\]có:

\( \Rightarrow \frac{{IE}}{{IC}} = \frac{{IM}}{{IE}} \Leftrightarrow I{E^2} = IC.IM\left( 2 \right)\)

Từ (1) và (2) \( \Rightarrow IK.ID = IC.IM \Rightarrow \frac{{IK}}{{IM}} = \frac{{IC}}{{ID}}\)

Xét \(\Delta IMK\)và \[\Delta IDC\]có:

   mà \(\widehat {IDC} = 90^\circ \Rightarrow \widehat {IMK} = 90^\circ \Rightarrow CI \bot KM\).