Một tháp nước được xây dựng trên một con dốc nghiêng \(6^\circ \) so với phương ngang. Để tháp đứng thẳng, người ta dùng hai dây cáp cố định (hình vẽ). Biết rằng tháp cao \(24m\) và khoảng cách từ chân thấp đến chỗ cố định dây cáp là \(18m\). Hỏi dây cáp dài hơn có chiều dài bằng bao nhiêu (làm tròn kết quả đến hàng phần mười của mét)?
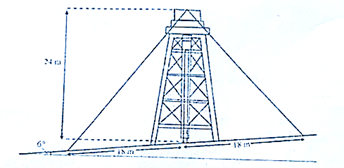
Một tháp nước được xây dựng trên một con dốc nghiêng \(6^\circ \) so với phương ngang. Để tháp đứng thẳng, người ta dùng hai dây cáp cố định (hình vẽ). Biết rằng tháp cao \(24m\) và khoảng cách từ chân thấp đến chỗ cố định dây cáp là \(18m\). Hỏi dây cáp dài hơn có chiều dài bằng bao nhiêu (làm tròn kết quả đến hàng phần mười của mét)?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án:
31,5
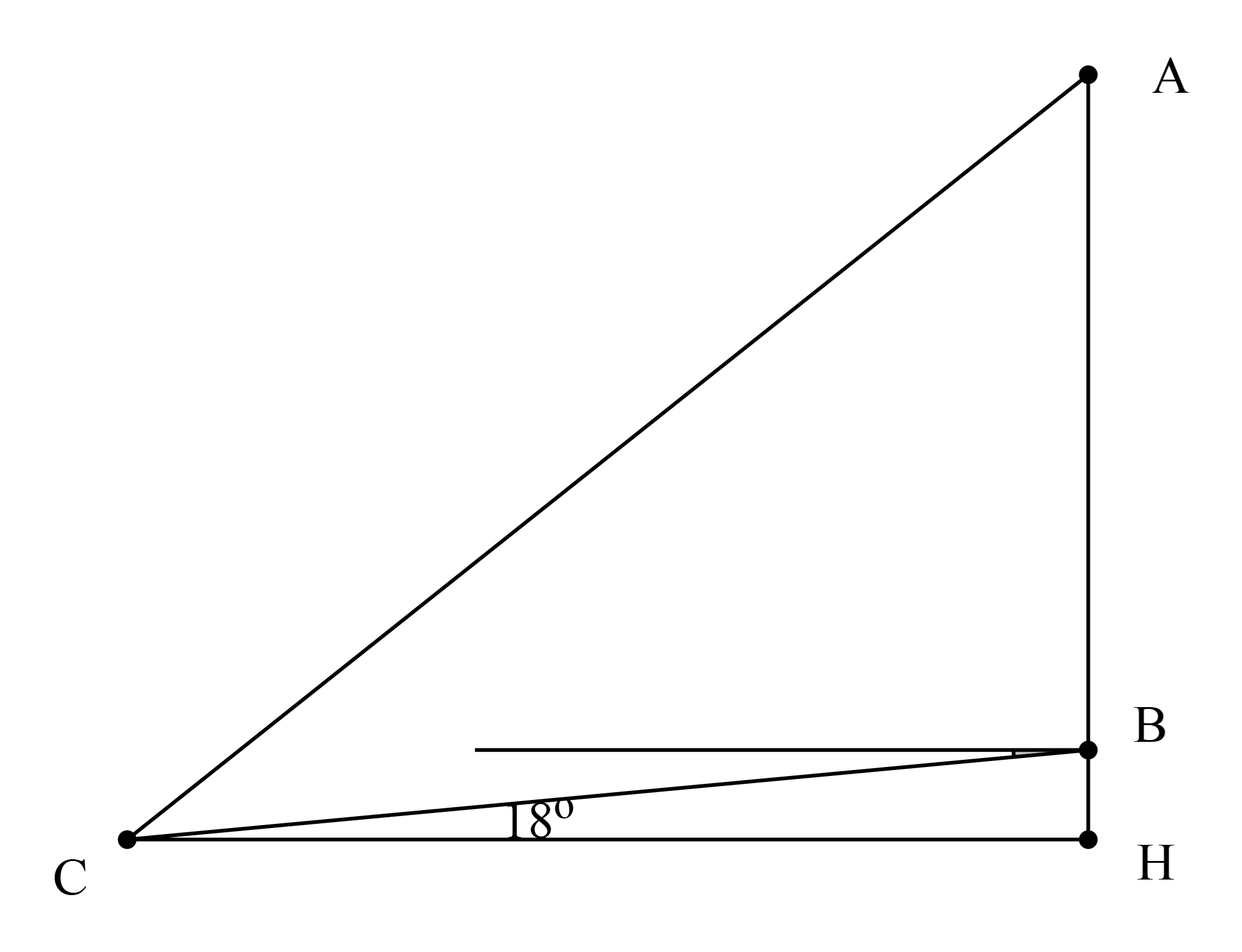
Ta có: \(BH = 18.\sin 18^\circ \left( m \right)\); \(CH = 18.\cos 18^\circ \); \(AH = AB + BH = 24 + 18.\sin 18^\circ \)
Áp dụng định lý Pythagore cho tam giác \(AHC\) là: \(A{C^2} = A{H^2} + C{H^2}\)
Chiều dài dây cáp dài hơn là gần bằng \(31,5m\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
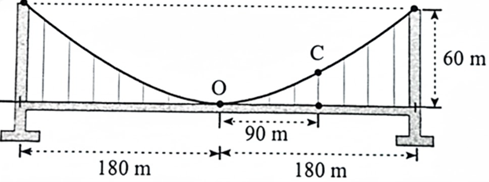
Gọi phương trình parabol: \(y = a{x^2}\) (\(a \ne 0\)).
Vì parabol đi qua điểm \(\left( {90;60} \right)\) nên \(a{.180^2} = 60 \Rightarrow a = \frac{{60}}{{180.180}} = \frac{1}{{540}}\).
Độ cao của dây cáp tại vị trí \(C\) (cách tâm \(O\) của mặt cầu \(90m\) theo phương ngang) so với mặt cầu là: \(y = \frac{1}{{540}}{.90^2} = 15\) (m)
Đáp số: \(15m\)
Lời giải
Chọn C
Câu 3
a) Tứ giác \(CADB\) là tứ giác nội tiếp.
Đúng
Sai
b) \(OB = 3cm\)
Đúng
Sai
c) \(\widehat {ADB} = 45^\circ \)
Đúng
Sai
d) Diện tích của hình giới hạn bới hai tiếp tuyến \(MA,MB\) và cung nhỏ \(AB\) (phần tô đạm trong hình vẽ) bằng \(3\left( {3\sqrt 3 - \pi } \right)c{m^2}\).
Đúng
Sai
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(4x < 4y\).
B. \(x - y < 0\).
C. \( - x > - y\).
D. \(x - 3 > y - 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{x}{y} = \frac{5}{7}\).
B. \(\frac{x}{5} = \frac{y}{7}\)
C. \(\frac{x}{5} = \frac{7}{y}\).
D. \(\frac{x}{7} = \frac{y}{5}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[12\]cm.
B. \[\frac{{160}}{3}\]cm.
C. \(32\)cm.
D. \(\frac{{100}}{3}\)cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập