Cho tam giác \(ABC\) nhọn, nội tiếp đường tròn \(\left( O \right)\) và có đường cao \[AH.\] Kẻ \(HD \bot AB\) và \(HE \bot AC{\rm{ }}\left( {D \in AB,{\rm{ }}E \in AC} \right).\) Gọi đường thẳng \[d\] là tiếp tuyến của đường tròn \(\left( O \right)\) tại \[A\].
Quảng cáo
Trả lời:
a) Đ b) Đ c) Đ d) S
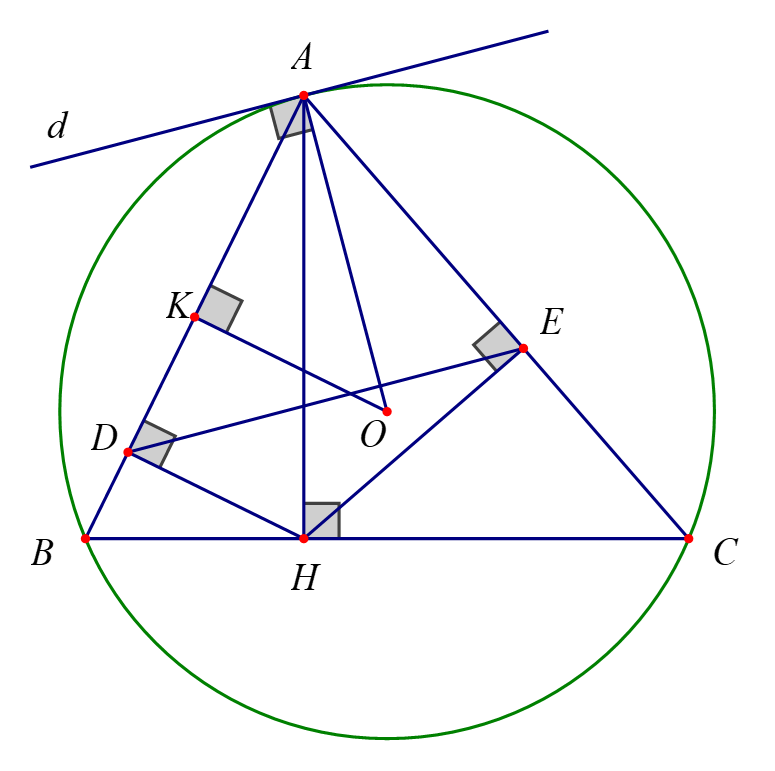
a) Ta có: \[\widehat {ADH} = \widehat {AEH} = 90^\circ \]
\[ \Rightarrow \] Tứ giác \(ADHE\) nội tiếp đường tròn đường kính \(AH\). Do đó a) Đúng.
b) Ta có: đường thẳng \[d\] là tiếp tuyến của đường tròn \(\left( O \right)\) tại \[A\] (gt)
\[ \Rightarrow d \bot OA\]. Do đó b) Đúng.
c) Ta có: (1)
(2)
Từ (1), (2) suy ra \[ \Rightarrow \widehat {ADE} = \widehat {AEB} = 40^\circ \].
mà \[\widehat {ADE} + \widehat {BDE} = 180^\circ \] (2 góc kề bù) \[ \Rightarrow \widehat {BDE} = 140^\circ \]. Do đó c) Đúng.
d) Kẻ \[OK \bot AB\;\left( {K \in AB} \right)\].
Ta có: \[\widehat {dAB} + \widehat {BAO} = \widehat {AOK} + \widehat {KAO}\;\left( { = 90^\circ } \right) \Rightarrow \widehat {dAB} = \widehat {AOK} = \frac{1}{2}\widehat {AOB}\]
mà \[\widehat {ACB} = \frac{1}{2}\widehat {AOB} \Rightarrow \widehat {dAB} = \widehat {ACB}\]
mà \[\widehat {ADE} = \widehat {ACB}\] (cm câu c) \[ \Rightarrow \widehat {dAB} = \widehat {ADE} \Rightarrow d\;{\rm{//}}\;DE\]. Do đó d) Sai.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 172
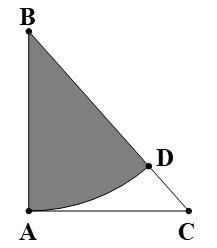
Ta có: \[{S_{\Delta ABC}} = \frac{1}{2}AB\,.\,AC = \frac{1}{2}\, \cdot \,40\, \cdot \,40 = 800\;\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
\[{S_{qt}} = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi \,.\,{{40}^2}\,.\,45}}{{360}} = 200\pi \;\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Ta có diện tích trồng cỏ bằng
\[{S_{\Delta ABC}} - {S_{qt}} = 800 - 200\pi \approx 172\;\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Câu 2
A. \[ - 3\].
Lời giải
Đáp án đúng là C
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
d) Với \(x < 5\) thì rút gọn biểu thức đã cho ta được \(P = x - 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.