Câu hỏi:

02/02/2026 58

Cho Parabol $(P):y = - {x^2}$ và đường thẳng (d): $y = 5x + 6$

a) Vẽ đồ thị (P).

b) Tìm tọa độ các giao điểm của (P) và (d) bằng phép tính.

Xem lời giải

Câu hỏi trong đề: 46 bài tập Toán 9 Kết nối tri thức Bài 19. Phương trình bậc hai một ẩn có đáp án !!

Quảng cáo

Trả lời:

Giải bởi Vietjack

a) Vẽ đồ thị $\left( P \right)$.

Đồ thị hàm số $y = - {x^2}$ đi qua gốc tọa độ $O$, có bề lõm hướng xuống và nhận $Oy$ làm trục đối xứng.

Bảng giá trị:

$x$	$ - 2$	$ - 1$	0	1	2
$y = - {x^2}$	$ - 4$	$ - 1$	0	$ - 1$	$ - 4$

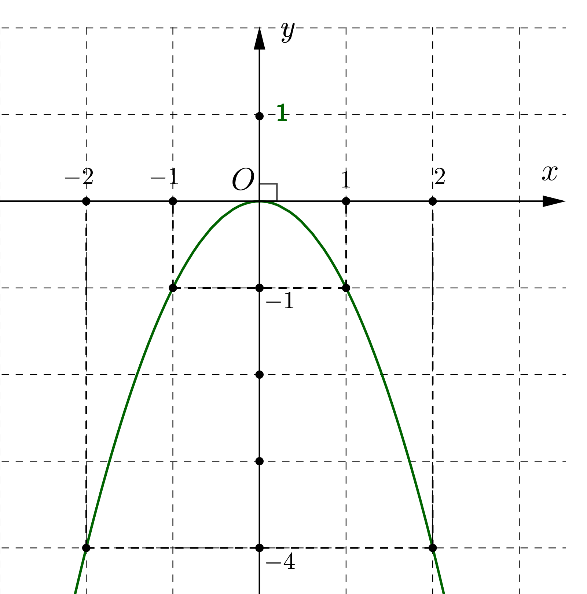
$ \Rightarrow $ Parabol $\left( P \right):y = - {x^2}$ đi qua các điểm $\left( { - 2; - 4} \right)$, $\left( { - 1; - 1} \right)$, $\left( {0;0} \right)$, $\left( {1; - 1} \right)$, $\left( {2; - 4} \right)$.

Đồ thị Parabol $\left( P \right):y = - {x^2}$:

$Cho Parabol $(P):y = - {x^2}$ và đường thẳng (d): $y = 5x + 6$ a) Vẽ đồ thị (P). b) Tìm tọa độ các giao điểm của (P) và (d) bằng phép tính. (ảnh 1)$

Hoành độ giao điểm của đồ thị $(P)$ và $(d)$là nghiệm của phương trình:

$\begin{array}{l} - {x^2} = 5x + 6\\{x^2} + 5x + 6 = 0\end{array}$

Ta có: ${\rm{\Delta }} = {b^2} - 4ac = {5^2} - 4.6 = 1 > 0$ nên phương trình có 2 nghiệm phân biệt

$\begin{array}{l}{x_1} = \frac{{ - 5 + 1}}{2} = - 2\\{x_2} = \frac{{ - 5 - 1}}{2} = - 3\end{array}$.

Với ${x_1} = - 2 \Rightarrow {y_1} = - {( - 2)^2} = - 4$.

Với ${x_2} = - 3 \Rightarrow {y_2} = - {( - 3)^2} = - 9$.

Vậy tọa độ các giao điểm của $\left( P \right)$ và (d) là $A\left( { - 2; - 4} \right),B\left( { - 3; - 9} \right)$.

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Hai công nhân cùng làm một công việc thì hoàn thành công việc đó trong 6 giờ 40 phút. Nếu họ làm riêng thì công nhân thứ nhất hoàn thành công việc đó ít hơn công nhân thứ hai là 3 giờ. Hỏi nếu làm riêng thì mỗi công nhân phải làm trong bao lâu thì xong việc?

Xem đáp án

Lời giải

Ta có 6 giờ 40 phút $ = 6\frac{2}{3}$ giờ.

Gọi thời gian công nhân thứ nhất làm một mình xong công việc là $x$ (giờ, $x > 6\frac{2}{3}$ ).

Thời gian công nhân thứ hai làm một mình xong việc là $x + 3$ (giờ).

Mỗi giờ công nhân thứ nhất làm được $\frac{1}{x}$ (công việc).

Mỗi giờ công nhân thứ hai làm được $\frac{1}{{x + 3}}$ (công việc).

Theo đầu bài, hai công nhân cùng làm thì hoàn thành công việc trong $6\frac{2}{3}$ giờ. Nên mỗi giờ họ cùng làm được $1:6\frac{2}{3} = \frac{3}{{20}}$ (công việc). Ta có phương trình:

$\frac{1}{x} + \frac{1}{{x + 3}} = \frac{3}{{20}} \Leftrightarrow 3{x^2} - 31x - 60 = 0$.

Ta có $\Delta = {31^2} - 4.3.( - 60) = 1681 > 0$ nên phương trình có nghiệm là ${x_1} = - \frac{5}{3}($loại$);{x_2} = 12$ (nhận).

Vậy thời gian công nhân thứ nhất làm xong công việc là 12 giờ. Thời gian công nhân thứ hai làm một mình xong công việc là 15 giờ.

Câu 2

Trong mặt phẳng tọa độ $Oxy$ cho Parabol $\left( P \right):y = {x^2}$, trên $\left( P \right)$ lấy hai điểm $A\left( { - 1;1} \right),B\left( {3;9} \right)$.

a) Tính diện tích tam giác $OAB$.

b) Xác định điểm $C$ thuộc cung nhỏ $AB$ của $\left( P \right)$ sao cho diện tích tam giác $ABC$ lớn nhất.

Xem đáp án

Lời giải

a) Gọi $y = ax + b$ là phương

trình đường thẳng $AB$.

Ta có $\left\{ \begin{array}{l}a.\left( { - 1} \right) + b = 1\\a.3 + b = 9\end{array} \right. \Rightarrow \left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.$

suy ra phương trình đường thẳng $AB$$\left( d \right):y = 2x + 3$.

Đường thẳng $AB$ cắt trục $Oy$ tại điểm $I\left( {0;3} \right)$.

$Trong mặt phẳng tọa độ $Oxy$ cho Parabol \(\left( (ảnh 1)$

Diện tích tam giác $OAB$ là: ${S_{OAB}} = {S_{OAI}} + {S_{OBI}} = \frac{1}{2}AH.OI + \frac{1}{2}BK.OI$.

Ta có $AH = 1;BK = 3,OI = 3$.

Suy ra ${S_{OAB}} = 6$ (đvdt).

b) Giả sử $C\left( {c;{c^2}} \right)$ thuộc cung nhỏ $\left( P \right)$ với $ - 1 < c < 3$.

Diện tích tam giác:${S_{ABC}} = {S_{ABB'A'}} - {S_{ACC'A'}} - {S_{BCC'B'}}$.

Các tứ giác $ABB'A',AA'C'C,CBB'C'$ đều là hình thang vuông nên ta có:

${S_{ABC}} = \frac{{1 + 9}}{2}.4 - \frac{{1 + {c^2}}}{2}.\left( {c + 1} \right) - \frac{{9 + {c^2}}}{2}.\left( {3 - c} \right) = 8 - 2{\left( {c - 1} \right)^2} \le 8$.

Vậy diện tích tam giác $ABC$ lớn nhất bằng $8$ (đvdt) khi $C\left( {1;1} \right)$.

Câu 3