Người ta vẽ bảng quy hoạch của một khu định cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là \(900\;{\rm{m}},1200\;{\rm{m}}\) và 1500 m (Hình vẽ).
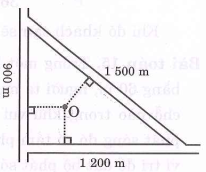
a) Tính chu vi và diện tích của phần đất giới hạn bởi tam giác trên.
b) Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?
Người ta vẽ bảng quy hoạch của một khu định cư được bao xung quanh bởi ba con đường thẳng lập thành một tam giác với độ dài các cạnh là \(900\;{\rm{m}},1200\;{\rm{m}}\) và 1500 m (Hình vẽ).

a) Tính chu vi và diện tích của phần đất giới hạn bởi tam giác trên.
b) Họ muốn xây dựng một khách sạn bên trong khu dân cư cách đều cả ba con đường đó. Hỏi khi đó khách sạn sẽ cách mỗi con đường một khoảng là bao nhiêu?
Câu hỏi trong đề: 6 bài tập Toán thực tế (có lời giải) !!
Quảng cáo
Trả lời:
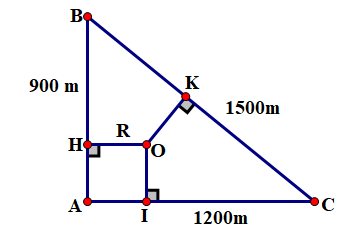
a) Xét tam giác ABC , ta có: \({\rm{B}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{A}}{{\rm{C}}^2}\left( {{{1500}^2} = {{900}^2} + {{1200}^2}} \right)\)
Theo định lí Pythagore đảo, tam giác ABC vuông tại A .
Phần đất giới hạn là tam giác vuông, gọi P là chu vi, ta có: \(P = AB + BC + AC = 900 + 1500 + 1200 = 3600(m)\)
Và diện tích \({{\rm{S}}_{{\rm{ABC}}}} = \frac{1}{2} \cdot {\rm{AB}} \cdot {\rm{AC}} = \frac{1}{2} \cdot 900 \cdot 1200 = 540000\left( {\;{{\rm{m}}^2}} \right)\)
b) Gọi O là nơi xây dựng khách sạn và khoảng cách từ khách sạn đến ba con đường là \({\rm{OH}} = {\rm{OI}} = {\rm{OK}} = {\rm{R}}\).
Ta có: \({{\rm{S}}_{{\rm{ABC}}}} = {{\rm{S}}_{{\rm{AOB}}}} + {{\rm{S}}_{{\rm{AOC}}}}\) (trong đó \({{\rm{S}}_{{\rm{AOB}}}},{{\rm{S}}_{{\rm{AOC}}}},{{\rm{S}}_{{\rm{BOC}}}}\) lần lượt là diện tích các tam giác AOB, AOCvà BOC)
\({{\rm{S}}_{{\rm{ABC}}}} = \frac{1}{2}{\rm{R}} \cdot {\rm{AB}} + \frac{1}{2}{\rm{R}} \cdot {\rm{AC}} + \frac{1}{2}R \cdot BC\)
\({{\rm{S}}_{{\rm{ABC}}}} = \frac{1}{2}{\rm{R}}({\rm{AB}} + {\rm{AC}} + {\rm{BC}})\)
\({{\rm{S}}_{{\rm{ABC}}}} = \frac{1}{2}{\rm{R}} \cdot {\rm{P }}\) (\({{\rm{S}}_{{\rm{ABC}}}}\)là diện tích và \(P\) là chu vi)\( \Rightarrow {\rm{R}} = \frac{{2 \cdot \;{{\rm{S}}_{{\rm{ABC}}}}}}{{\rm{P}}} = \frac{{2.540000}}{{3600}} = 300(\;{\rm{m}})\)
Khi đó khách sạn sẽ cách mỗi con đường 300 (m).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
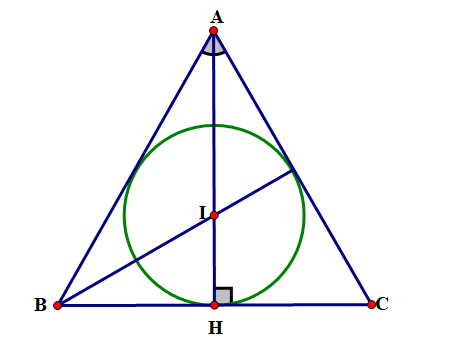
Gọi I là tâm của đường tròn nội tiếp tam giác đều ABC .
Kẻ đường cao AH , khi đó tâm I của đường tròn nội tiếp (giao điểm của ba đường phân giác cũng là trọng tâm).
Ta có AH là đường trung tuyến\( \Rightarrow {\rm{H}}\)là trung điểm của BC hay \({\rm{BH}} = {\rm{CH}} = \frac{{{\rm{BC}}}}{2} = \frac{{12}}{2} = 6\) (m).
Xét tam giác BHI vuông tại H . Có \({\rm{BH}} = 6\;{\rm{cm}}\) và
Theo định lí về hệ thức lượng trong tam giác vuông, ta có:
Vậy bán kính của phần đất trồng hoa là \({\rm{r}} = 2\sqrt 3 (\;{\rm{m}})\)
Do đó diện tích phần đất trồng hoa là \({\rm{S}} = \pi \cdot {(2\sqrt 3 )^2} = 12\pi \left( {\;{{\rm{m}}^2}} \right)\)
Lời giải
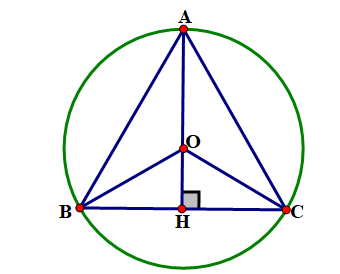
Gọi O là vị trí cách đều ba vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\) nên O là tâm đường tròn ngoại tiếp tam giác ABC (giao điểm của ba đường trung trực).
Do đều (gt) nên O đồng thời là trực tâm và trọng tâm của tam giác hay AH là đường cao của tam giác ABC
đều cạnh 15 m .\( \Rightarrow {\rm{AH}} = \frac{{15\sqrt 3 }}{2}(\;{\rm{m}})\) vì AH đồng thời là trung tuyến của có trọng tâm O\( \Rightarrow {\rm{OA}} = \frac{2}{3}{\rm{AH}} = \frac{2}{3} \cdot \frac{{15\sqrt 3 }}{2} = 5\sqrt 3 (\;{\rm{m}})\).
Vậy khoảng cách từ vị trí O đến mỗi vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\) là \(5\sqrt 3 (\;{\rm{m}})\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.