Cẩu tháp là một loại thiết bị nâng hạ được thiết kế để nâng, hạ và di chuyển vật liệu xây dựng tại các công trường, đặc biệt là trong xây dựng các công trình cao tầng. Có khả năng hoạt động ở độ cao lớn và với tải trọng nặng, cẩu tháp được lắp đặt cố định hoặc có thể di chuyển trên ray tại công trường, giúp tăng hiệu quả công việc và đảm bảo an toàn lao động.

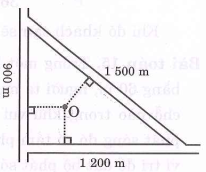
Ba vị trí \(A,B,C\) của một công trình là ba đỉnh của một tam giác đều. Trên công trình, người ta muốn đặt cẩu tháp tại điểm \(O\) sao cho bán kính quay của cẩu tháp đến các vị trí điểm \(A,B,C\) bằng nhau và bằng 60 m (hình bên). Tính khoảng cách từ \(A\) đến \(B\) (làm tròn đến số hàng đơn vị).

                               

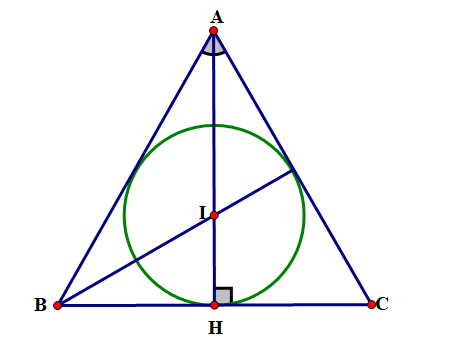
Gọi I là tâm của đường tròn nội tiếp tam giác đều ABC .

Kẻ đường cao AH , khi đó tâm I của đường tròn nội tiếp (giao điểm của ba đường phân giác cũng là trọng tâm).

Ta có AH là đường trung tuyến\( \Rightarrow {\rm{H}}\)là trung điểm của BC hay \({\rm{BH}} = {\rm{CH}} = \frac{{{\rm{BC}}}}{2} = \frac{{12}}{2} = 6\) (m).

Xét tam giác BHI vuông tại H . Có \({\rm{BH}} = 6\;{\rm{cm}}\) và $\widehat{\text{IBH}}={30}^{°}$

Theo định lí về hệ thức lượng trong tam giác vuông, ta có: $\text{IH}=\text{BH}\cdot \tan \text{IBH}=6\cdot \tan {30}^{°}=2\sqrt{3}( \text{m})$

Vậy bán kính của phần đất trồng hoa là \({\rm{r}} = 2\sqrt 3 (\;{\rm{m}})\)

Do đó diện tích phần đất trồng hoa là \({\rm{S}} = \pi \cdot {(2\sqrt 3 )^2} = 12\pi \left( {\;{{\rm{m}}^2}} \right)\)

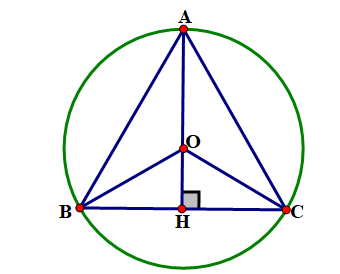
Gọi O là vị trí cách đều ba vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\) nên O là tâm đường tròn ngoại tiếp tam giác ABC (giao điểm của ba đường trung trực).

Do $△\text{ABC}$đều (gt) nên O đồng thời là trực tâm và trọng tâm của tam giác hay AH là đường cao của tam giác ABC

đều cạnh 15 m .\( \Rightarrow {\rm{AH}} = \frac{{15\sqrt 3 }}{2}(\;{\rm{m}})\) vì AH đồng thời là trung tuyến của có trọng tâm O\( \Rightarrow {\rm{OA}} = \frac{2}{3}{\rm{AH}} = \frac{2}{3} \cdot \frac{{15\sqrt 3 }}{2} = 5\sqrt 3 (\;{\rm{m}})\).

Vậy khoảng cách từ vị trí O đến mỗi vị trí \({\rm{A}},{\rm{B}},{\rm{C}}\) là \(5\sqrt 3 (\;{\rm{m}})\).