Cho biết cạnh hình vuông lớn bằng 8 cm. Tính diện tích phần tô màu xanh trong hình vẽ bên:
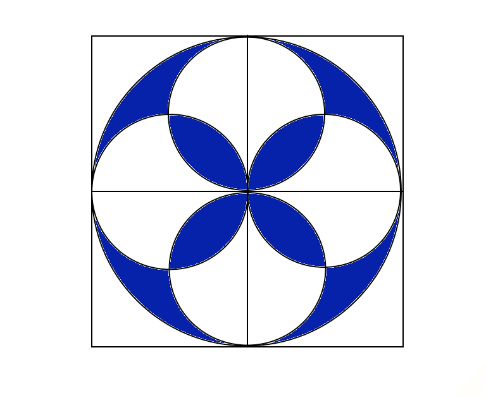
Cho biết cạnh hình vuông lớn bằng 8 cm. Tính diện tích phần tô màu xanh trong hình vẽ bên:

Quảng cáo
Trả lời:
Ta chia hình vuông ban đầu thành 4 phần bằng nhau. Bây giờ ta tính diện tích phần tô đậm nằm trong hình vuông \({O_1}\) ( \(\frac{1}{4}\) diện tích hình đã cho).
Diện tích phần tô đậm trong hình vuông \({O_1}\) là: \(S = {S_1} + {S_3} + {S_4}\).
Ta thấy: \({S_2} = {S_4} = {S_3} = {S_5}\) (Vì đều bằng \(\frac{1}{4}\) diện tích hình tròn bán kính 2 cm trừ đi diện tích hình tam giác vuông có hai cạnh góc vuông bằng 2 cm).
Nên \(S = {S_1} + {S_2} + {S_5}\) và bằng \(\frac{1}{4}\) diện tích hình tròn bán kính 4 cm trừ đi diện tích hình tam giác vuông có hai cạnh góc vuông bằng 4 cm . Ta có: \(S = 4.4.\pi .\frac{1}{4} - \frac{1}{2}.4.4 \approx 4,57\left( {\;c{m^2}} \right)\).
Diện tích phần tô đậm cần tìm là: \(4,57.4 \approx 18,28\left( {\;{\rm{c}}{{\rm{m}}^2}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
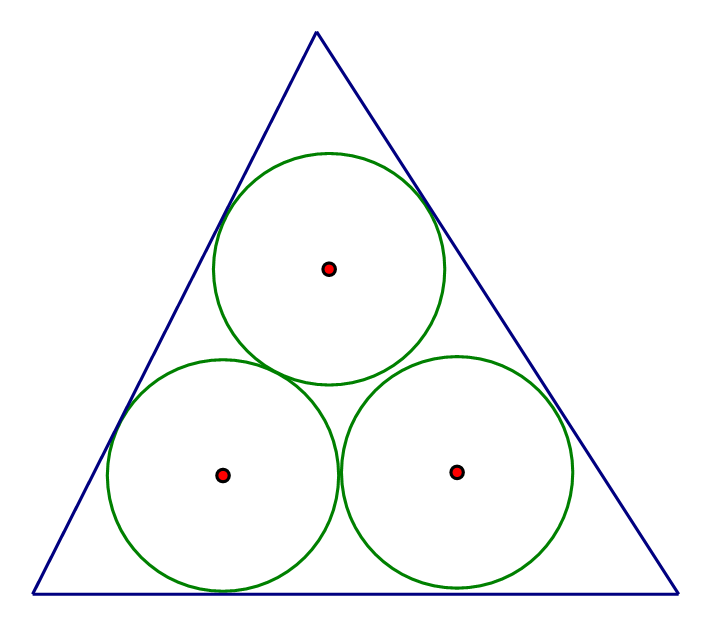
Từ tâm \[P\] và \[Q\] vẽ \[PQ\] và \[CQ\] vuông góc với cạnh \[AD\] của tam giác
Các tam giác \[APB\] và \[DQC\] là nửa tam giác đều với \[PB = QC = 3\]
\[ \Rightarrow AB = CD = 3\sqrt 3 ;BC = PQ = 6 \Rightarrow AD = 6 + 6\sqrt 3 \]
Vậy chu vi tam giác là: \[18 + 18\sqrt 3 \]
Lời giải
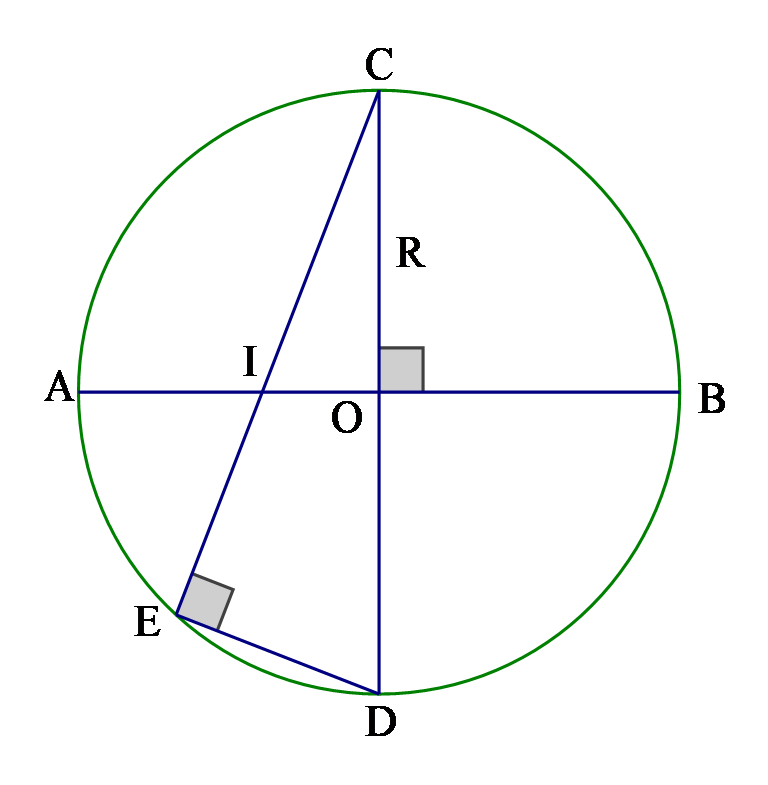
Ta có \(AI = \frac{{2AO}}{3} = \frac{{2R}}{3} \Rightarrow OI = R - \frac{{2R}}{3} = \frac{R}{3}\)
\(\Delta OCI\) vuông tại \(O\), ta có:
\(CI = \sqrt {O{C^2} + O{I^2}} = \sqrt {{R^2} + {{\left( {\frac{R}{3}} \right)}^2}} = \frac{{R\sqrt {10} }}{3}\)
\(\Delta CED\) nội tiếp đường tròn \(O\) có cạnh \(CD\) là đường kính \( \Rightarrow \Delta CED\) vuông tại \(E\)
Hai tam giác vuông \(OCI\) và \(CED\) có \(\widehat C:chung\)
\( \Rightarrow \Delta COI \sim \Delta CED \Rightarrow \frac{{CO}}{{CE}} = \frac{{CI}}{{CD}} \Rightarrow CE = \frac{{CO.CD}}{{CI}}\)
\( = \frac{{R.2R}}{{R\frac{{\sqrt {10} }}{3}}} = \frac{{6R}}{{\sqrt {10} }} = \frac{{3R\sqrt {10} }}{5}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.