Cho parabol \(\left( P \right):y = {x^2}.\)
Cho parabol \(\left( P \right):y = {x^2}.\)
a) Diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\], \[Ox\] và 2 đường thẳng \[x = 0,\,\,x = 1\] bằng 1.
b) Diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\], đường thẳng \[\Delta :y = 2x\] và 2 đường thẳng \[x = 0,\,\,x = 2\] bằng 3.
c) Diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\], đường thẳng \[d:y = 3x - 2\]bằng 4.
d) Cho parabol \(\left( P \right):y = {x^2}\) và hai điểm \(A,B\) thuộc \(\left( P \right)\) sao cho \(AB = 2\). Diện tích lớn nhất của hình phẳng giới hạn bởi \(\left( P \right)\)và đường thẳng \(AB\) là \[\frac{4}{3}.\]
Câu hỏi trong đề: Đề kiểm tra Tích phân (có lời giải) !!
Quảng cáo
Trả lời:
a) Diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\], \[Ox\] và 2 đường thẳng\[x = 0,\,\,x = 1\] được xác định bởi công thức:\[S = \int\limits_0^1 {{x^2}{\rm{d}}x} = \frac{1}{3}.\]
Vậy khẳng định a) là sai.
b) Diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\], đường thẳng \[\Delta :y = 2x\] và 2 đường thẳng \[x = 0,\,\,x = 2\] được xác định bởi công thức: \[S = \int\limits_0^2 {\left| {{x^2} - 2x} \right|{\rm{d}}x} = \frac{4}{3}.\]
Vậy khẳng định b) là sai.
c) Xét phương trình hoành độ giao điểm của đường thẳng \[d\] và đồ thị \[\left( P \right):\]
\[{x^2} = 3x - 2 \Leftrightarrow {x^2} - 3x + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 2\end{array} \right..\]
Diện tích hình phẳng giới hạn bởi đồ thị \[\left( P \right)\], đường thẳng \[d:y = 3x - 2\] được xác định bởi công thức: \[S = \int\limits_1^2 {\left| {{x^2} - 3x + 2} \right|{\rm{d}}x} = \frac{1}{6}.\]
Vậy khẳng định c) là sai.
d) Gọi phương trình đường thẳng \(AB\)là: \(y = ax + b\) \(\left( {a,b \in \mathbb{R}} \right)\)
Phương trình giao điểm của \(AB\)và \(\left( P \right)\)là: \({x^2} - ax - b = 0\)
Để có 2 điểm \(A,B\) thì \({a^2} + 4b > 0\). khi đó: \(\left\{ \begin{array}{l}A\left( {{x_1};a{x_1} + b} \right)\\B\left( {{x_2};a{x_2} + b} \right)\\{x_1} + {x_2} = a\\{x_1}{x_2} = - b\end{array} \right.\)
Nên \[AB = 2 \Leftrightarrow \sqrt {\left( {{a^2} + 1} \right)} \left| {{x_2} - {x_1}} \right| = 2\]
Giả sử \[{x_2} > {x_1}\] ta có \[\left| {{x_2} - {x_1}} \right| = \frac{2}{{\sqrt {\left( {{a^2} + 1} \right)} }} \le 2\]
Mặt khác: \[\left| {{x_2} - {x_1}} \right| = \sqrt {{{\left( {{x_2} + {x_1}} \right)}^2} - 4{x_1}{x_2}} = \sqrt {{a^2} + 4b} \]
Khi đó \[S = \int\limits_{{x_1}}^{{x_2}} {ax + b - {x^2}} {\rm{d}}x = \frac{a}{2}\left( {x_2^2 - x_1^2} \right) + b\left( {{x_2} - {x_1}} \right) - \frac{1}{3}\left( {x_2^3 - x_1^3} \right)\]
\[ = \left( {{x_2} - {x_1}} \right)\left[ {\frac{a}{2}\left( {{x_2} + {x_1}} \right) + b - \frac{1}{3}\left( {x_2^2 + {x_1}{x_2} + x_1^2} \right)} \right]\]
\[ = \left( {{x_2} - {x_1}} \right)\left[ {\frac{a}{2}.a + b - \frac{1}{3}\left( {{a^2} + b} \right)} \right]\]\[ = \left( {{x_2} - {x_1}} \right)\left[ {\frac{{{a^2}}}{b} + \frac{{2b}}{3}} \right]\]\[ = \frac{{{a^2} + 4b}}{6}\left( {{x_2} - {x_1}} \right)\]\[ = \frac{{{{\left( {{x_2} - {x_1}} \right)}^3}}}{6} \le \frac{8}{6} = \frac{4}{3}\].
Suy ra: \({S_{max}} = \frac{4}{3}\) khi \(\left\{ \begin{array}{l}a = 0\\{x_2} - {x_1} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_1} + {x_2} = 0\\{x_1} = {x_2} = 1\end{array} \right.\) (thỏa mãn vì \(\left( P \right)\) có tính đối xứng)
\[ \Rightarrow \left\{ \begin{array}{l}A\left( {1;1} \right)\\B\left( { - 1;1} \right)\end{array} \right.\] hoặc \(\left\{ \begin{array}{l}A\left( { - 1;1} \right)\\B\left( {1;1} \right)\end{array} \right.\).
Vậy khẳng định d) là đúng.Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
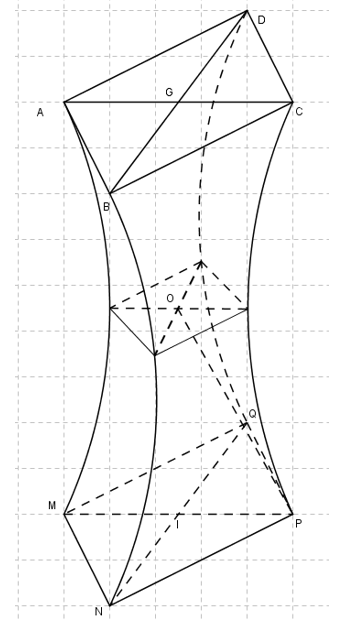
a)Diện tích đáy tòa nhà \({S_{ABCD}} = 1000\left( {{m^2}} \right).\)
b)Diện tích thiết diện hình vuông chính giữa (nhận O là tâm) bằng \(200\left( {{m^2}} \right).\)
c)Diện tích thiết diện \(ACPM\) bằng \(1200\left( {{m^2}} \right).\)
Lời giải
a)CHỌN SAI
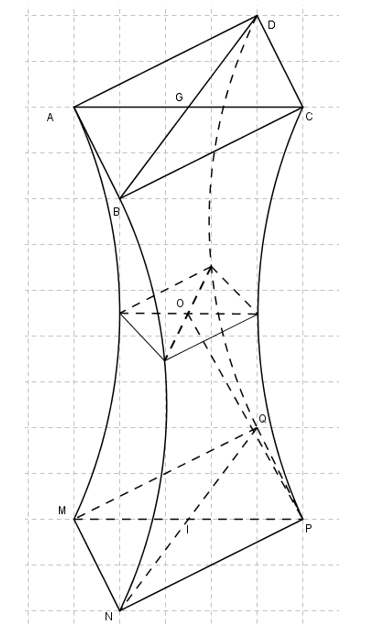
+)Chiều cao tòa nhà là \(48m \Rightarrow OI = 24m\)\( \Rightarrow IP = \sqrt {O{P^2} - O{I^2}} = \sqrt {{{30}^2} - {{24}^2}} = 18\)
+)\(PQ = 18\sqrt 2 = AB \Rightarrow {S_{ABCD}} = 648{m^2}\)
b)CHỌN ĐÚNG
Gọi L là tâm cung tròn như hình vẽ.
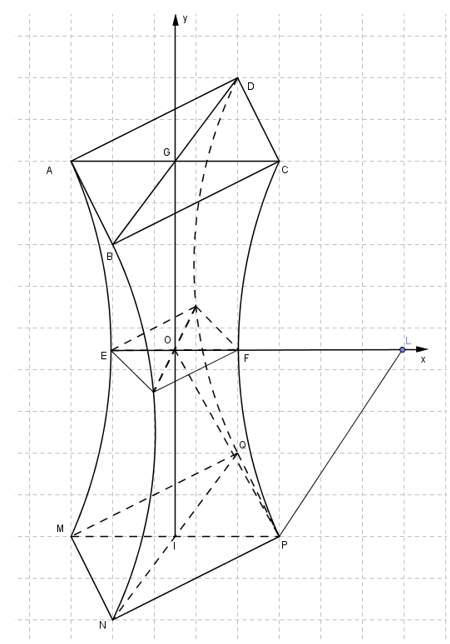
+)Ta tính được
\(LP = 40 \Rightarrow LO = 50 \Rightarrow {\rm{OF}} = 10 \Rightarrow {S_{td}} = 200\left( {{m^2}} \right)\)
c)CHỌN ĐÚNG.
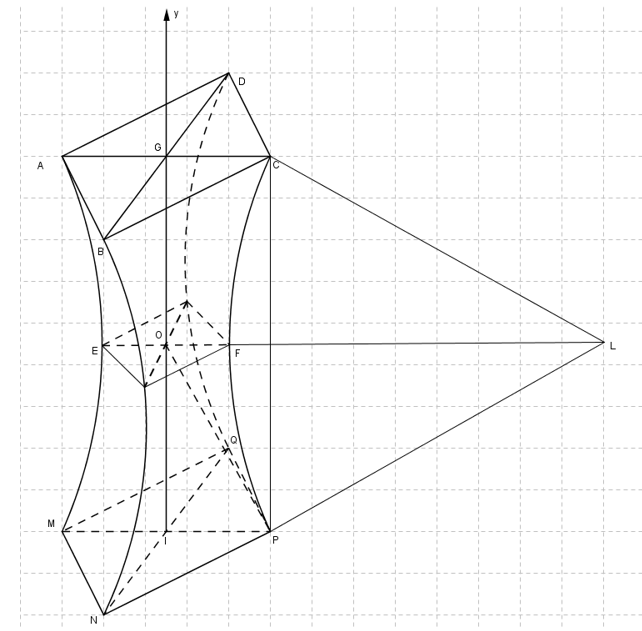
Ta có \({S_{LCP}} = 768\) và \(\cos \widehat {CLP} = \frac{{{{40}^2} + {{40}^2} - {{48}^2}}}{{2.40.40}} = \frac{7}{{25}} \Rightarrow \widehat {CLP} \approx 1,29(rad)\).
+)Diện tích quạt tròn \(LCFP\) là \({S_{LCFP}} = \frac{{1,{{29.40}^2}}}{2} = 1032\left( {{m^2}} \right)\)
+) Diện tích tam giác cong \(CFP\)là \({S_{CFP}} = 1032 - 768 = 264\left( {{m^2}} \right)\)\( \Rightarrow {S_{ACPM}} = 2\left( {{S_{GCPI}} - {S_{CFP}}} \right) = 2\left( {48.18 - 264} \right) = 1200\left( {{m^2}} \right)\)
d)CHỌN ĐÚNG.
Chọn hệ trục như hình vẽ.
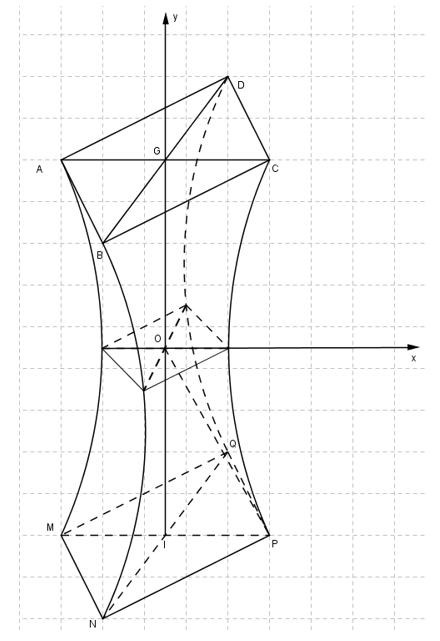
+)Phương trình đường tròn \[\left( {L;40} \right)\] là \[{\left( {x - 50} \right)^2} + {y^2} = 1600 \Rightarrow x = 50 - \sqrt {1600 - {y^2}} \].
+)Độ dài đường chéo thiết diện phẳng cắt bởi mặt phẳng vuông góc với Oy là
\[2\left( {50 - \sqrt {1600 - {y^2}} } \right)\]
Suy ra \[ \Rightarrow S\left( y \right) = {\left( {2\left( {50 - \sqrt {1600 - {y^2}} } \right)} \right)^2}\]
+)Vậy thể tích ngôi nhà là \[V = 2\int\limits_0^{24} {S\left( y \right){\rm{d}}y} = 2\int\limits_0^{24} {{{\left( {2\left( {50 - \sqrt {1600 - {y^2}} } \right)} \right)}^2}} .{\rm{d}}y = 31295\,\,\left( {{m^3}} \right)\].Lời giải
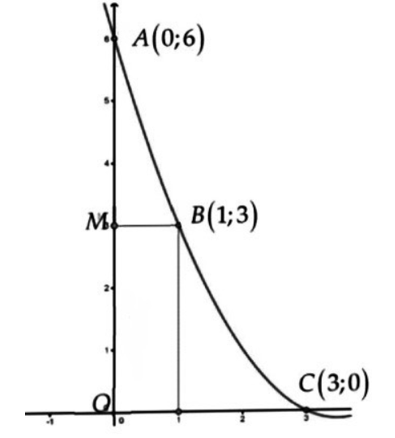
Đặt tọa độ như hình vẽ, ta có parabol cần tìm đi qua \(3\) điểm có toạn độ lần lượt là \(A\left( {0;6} \right),B\left( {1;3} \right),C\left( {3;0} \right)\) nên có phương trình là \(y = \frac{1}{2}{x^2} - \frac{7}{2}x + 6\)
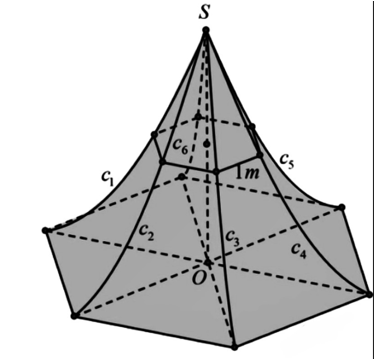
Theo hình vẽ ta có bán kính của bát giác là \(BM\).
Suy ra: \(2y = {x^2} - 7x + 12 \Rightarrow {\left( {x - \frac{7}{2}} \right)^2} = 2y + \frac{1}{4} \Rightarrow |x - \frac{7}{2}| = \sqrt {2y + \frac{1}{4}} \)
Mà \(x \in \left[ {0;3} \right] \Rightarrow \frac{7}{2} - x = \sqrt {2y + \frac{1}{4}} \)
Nếu ta đặt \(t = OM\)thì \(BM = \frac{7}{2} - \sqrt {2t + \frac{1}{4}} \)
Khi đó diện tích của thiết diện thiết diện lục giác:
\[S(t) = 6.\frac{{B{M^2}.\sqrt 3 }}{4} = \frac{{3\sqrt 3 }}{2}.{(\frac{7}{2} - \sqrt {2t + \frac{1}{4}} )^2}\] với \(t \in [0;6]\)
Vậy thể tích của mái chòi theo đề bài là:
\[V = \int\limits_0^6 {S(t)dt} = \int\limits_0^6 {\frac{{3\sqrt 3 }}{2}.{{(\frac{7}{2} - \sqrt {2t + \frac{1}{4}} )}^2}dt} = 29,2{m^3}\]Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
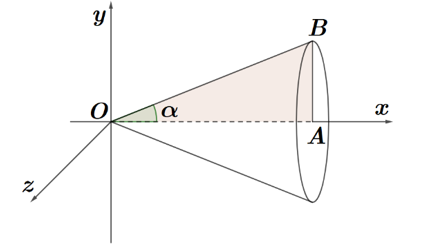
Câu 4
a) Khi \(\alpha = \frac{\pi }{4}\) thì \[OB = x\].
b) Khi \(\alpha = \frac{\pi }{6}\) thì thể tích \(V\) của khối \[\beta \] là \[\frac{{\pi {a^3}}}{9}\] (đvtt).
c) Khi thể tích \(V\) của khối \[\beta \] là \(\frac{{4\pi {a^3}}}{3}\) thì giá trị \(\cos \alpha < \frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Một vật chuyển động trong \(4\)giờ với vận tốc .\[\]. phụ thuộc vào thời gian (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/01/blobid39-1769864005.png)