Cho \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {x + 4} \), trục hoành và trục tung. Biết đường thẳng \(d:ax + by - 16 = 0\) đi
qua \(A\left( {0;2} \right)\) và chia \(\left( H \right)\) thành hai phần có diện tích bằng nhau (Hình bên). Giá trị \(a + b\) bằng
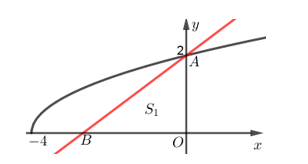
Cho \(\left( H \right)\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {x + 4} \), trục hoành và trục tung. Biết đường thẳng \(d:ax + by - 16 = 0\) đi
qua \(A\left( {0;2} \right)\) và chia \(\left( H \right)\) thành hai phần có diện tích bằng nhau (Hình bên). Giá trị \(a + b\) bằng

Câu hỏi trong đề: Đề kiểm tra Ôn tập chương 4 (có lời giải) !!
Quảng cáo
Trả lời:
Đáp án:
Phần giải chi tiết:
Gọi \(S\) là diện tích hình \(\left( H \right)\) suy ra \(S = \int\limits_{ - 4}^0 {\sqrt {x + 4} \,dx = \frac{{16}}{3}} \).
Gọi \({S_1}\) là diện tích hình \(\left( {{H_1}} \right)\) giới hạn bởi đường thẳng \(d\), trục tung và trục hoành.
Do \(d:ax + by - 16 = 0\) đi qua \(A\left( {0;2} \right)\) suy ra \(b = 8\).
Theo giả thiết thì \({S_1} = \frac{S}{2} = \frac{8}{3}\) mà \({S_1} = \frac{1}{2}OA.\,OB \Rightarrow OB = \frac{8}{3} \Rightarrow B\left( { - \frac{8}{3};0} \right)\).
Do \(B \in d \Rightarrow a = - 6\).
Vậy \(a + b = 2\).Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phần giải chi tiết
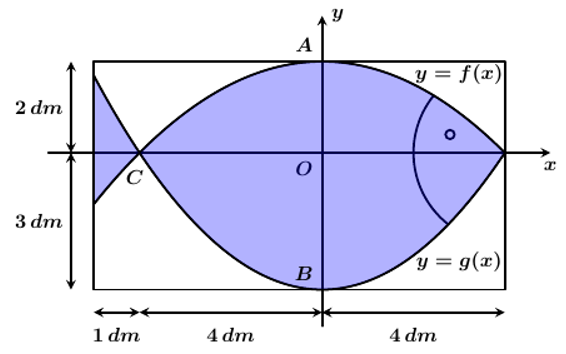
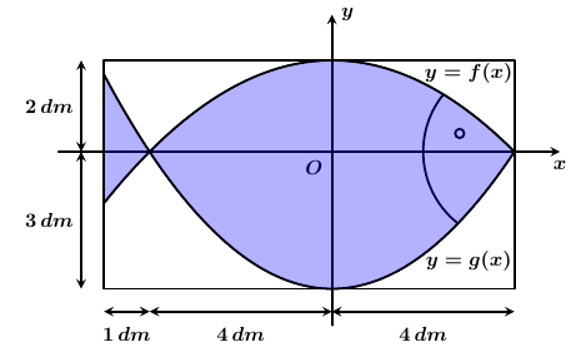
Dựa vào đồ thị, ta thấy:
+ Parabol \(y = f\left( x \right)\) có đỉnh là \(A\left( {0;2} \right)\) nên \(y = f\left( x \right) = a{x^2} + 2\)
Mặt khác, \(C\left( { - 4;0} \right)\) thuộc parabol \(y = f\left( x \right)\) nên \(y = f\left( x \right) = - \frac{1}{8}{x^2} + 2\)
+ Parabol \(y = g\left( x \right)\) có đỉnh là \(B\left( {0; - 3} \right)\) nên \(y = g\left( x \right) = b{x^2} - 3\)
Mặt khác, \(C\left( { - 4;0} \right)\) thuộc parabol \(y = g\left( x \right)\) nên \(y = g\left( x \right) = \frac{3}{{16}}{x^2} - 3\)
+ Diện tích logo hình con cá là: \({S_1} = \int_{ - 5}^4 {\left| {f\left( x \right) - f\left( x \right)} \right|dx} = \frac{{1345}}{{48}}\,\,\left( {d{m^2}} \right)\)
+ Diện tích phần được sơn màu trắng là: \({S_2} = 9.5 - {S_1} = \frac{{815}}{{48}}\,\,\left( {d{m^2}} \right)\)
+ Chi phí để trang trí là: \(20\,\,000.{S_1} + 10\,\,000.{S_2} \approx 730\,\,000\) (đồng).Lời giải
Chi phí để sản xuất \(x\) sản phẩm bằng \(C\left( x \right) = \int {C'\left( x \right)} {\rm{d}}x = {x^3} - 2{x^2} + 10x + C\)
Mà chi phí cố định ban đầu để sản xuất là 500 nghìn đồng
Suy ra \(C\left( 0 \right) = 500 \Rightarrow C = 500\)\( \Rightarrow C\left( x \right) = {x^3} - 2{x^2} + 10x + 500\)
Khi bán \(x\) sản phẩm, số tiền thu được là: \(270x\) (nghìn đồng).
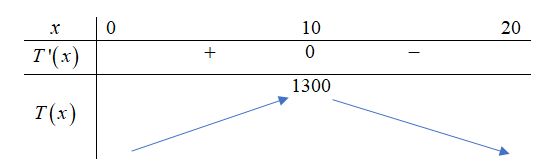
Do đó lợi nhuận thu được là: \(T\left( x \right) = - {x^3} + 2{x^2} + 260x - 500\) (nghìn đồng).
Ta có \(T'\left( x \right) = - 3{x^2} + 4x + 260 = 0 \Leftrightarrow x = 10{\rm{ }}\) hoặc \(x = - \frac{{26}}{3}\) (loại).
Bảng biến thiên
Câu 3
a) \[\int\limits_{ - 1}^2 {f\left( x \right)dx} = F\left( 2 \right) - F\left( { - 1} \right)\].
b) Nếu \(F\left( 0 \right) = 1\) thì \(F\left( 2 \right) = 12\).
c) Nếu \[\int\limits_0^2 {af\left( x \right)dx} = 32\] thì \(a = 6\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
a)\[\int\limits_{ - 1}^1 {f(x)dx = 8} \].
b) \[\int\limits_{ - 1}^4 {f(x)dx = 28} \].
c) Một vật chuyển động với phương trình \[v(t) = {t^2} - 4t + 5\]. Quãng đường vật đó đã di chuyển được từ lúc bắt đầu tới lúc gia tốc bị triệt tiêu là \[\frac{{14}}{3}\](m).
d) Một hoa văn trang trí được tạo ra từ một miếng bìa hình vuông cạnh \({\rm{30}}\,\,{\rm{cm}}\)bằng cách khoét đi bốn phần bằng nhau đều có hình dạng một nửa elip như hình vẽ. Biết một nửa trục lớn là \(AB = 8\)\({\rm{cm}}\), trục bé\(CD = 12\)\({\rm{cm}}\). Diện tích bề mặt của hoa văn đó bằng \[900 - 48\pi \left( {c{m^2}} \right)\].
![Cho hàm số \[y = f(x)\] có đồ thị như hình vẽ bên dưới: (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2026/02/blobid11-1769946390.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số \[y = f(x)\] có đồ thị như hình vẽ bên dưới: (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2026/02/blobid10-1769946350.png)