Câu hỏi trong đề: Sách bài tập Toán 7 Tập 2 !!
Quảng cáo
Trả lời:
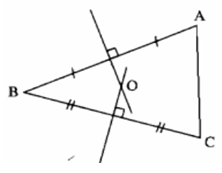
Vì điểm O cách đều hai điểm A và B nên O thuộc đường trung trực của AB.
Vì điểm O cách đều hai điểm A và C nên O thuộc đường trung trực của AC.
Vì điểm O cách đều hai điểm B và C nên O thuộc đường trung trực của BC.
Trong tam giác, ba đường trung trực đồng quy tại một điểm. Dựng đường trung trực AB và BC cắt nhau tại O.
Vậy O là điểm cần tìm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
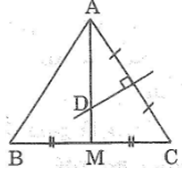
Vì ∆ABC cân tại A, AM là đường trung tuyến ứng với cạnh đáy BC nên AM cũng là đường trung trực của BC.
Vì D là giao điểm của các đường trung trực AC và BC nên D thuộc đường trung trực của AB.
Theo tính chất đường trung trực, ta có:
DA = DB.
Lời giải
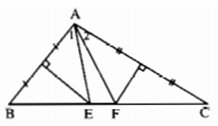
Vì E thuộc đường trung trực của đoạn thẳng AB nên EA = EB, hay tam giác EAB cân tại đỉnh E.
Suy ra : ∠A1 = ∠B (1)
Vì F thuộc đường trung trực của đoạn thẳng AC nên FA = FC, hay tam giác FAC cân tại đỉnh F. Suy ra : ∠A2 =∠C (2).
Từ (1) và (2) suy ra: ∠A1 + ∠A2 = ∠B + ∠C
Ta có:
∠(EAF) = ∠A − (∠A1 + ∠A2 ) = ∠A − (∠B + ∠C )
Mặt khác: ∠A + ∠B + ∠C = 1800 ( tổng ba góc của một tam giác )
suy ra: ∠B + ∠C = 180o − ∠A = 180o − 100o = 80o
Do đó ∠(EAF) = 100o − 80o = 20o
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.