Hình thoi ABCD có $\angle$A = ${60}^0$. Kẻ hai đường cao BE, BF. Tam giác BEF là tam giác gì? Vì sao?

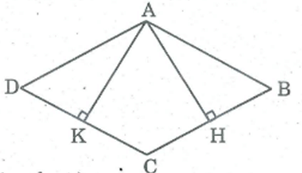
Xét hai tam giác vuông AHC và AKC, ta có:

$\angle$(AHC) = $\angle$(AKC) = ${90}^0$

AH = AK (gt)

AC cạnh huyền chung

Suy ra: $∆$AHC = $∆$AKC (cạnh huyền- cạnh góc vuông)

⇒ $\angle$(ACH) = $\angle$(ACK) hay $\angle$(ACB) = $\angle$(ACD)

⇒ CA là tia phân giác $\angle$(BCD)

Hình bình hành ABCD có đường chéo CA là đường phân giác nên là hình thoi.

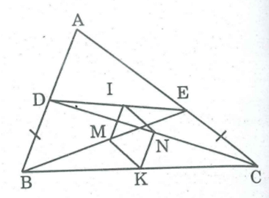
*Trong $∆$BCD,ta có:

K là trung điểm của BC (gt)

N là trung điểm của CD (gt)

Nên NK là đường trung bình của $∆$BCD

⇒ NK // BD và NK = 1/2 BD (1)

*Trong $∆$BED,ta có:

M là trung điểm của BE (gt)

I là trung điểm của DE (gt)

Nên MI là đường trung bình của $∆$BED

⇒ MI // BD và MI = 1/2 BD (t/chất đường trung bình trong tam giác) (2)

Từ (1) và (2) suy ra: MI // NK và MI = NK

Nên tứ giác MKNI là hình bình hành.

*Trong $∆$BEC ta có MK là đường trung bình.

⇒ MK = 1/2 CE (t/chất đường trung bình của tam giác)

BD = CE (gt). Suy ra: MK = KN

Vậy hình bình hành MKNI là hình thoi.

⇒IK ⊥ MN (t/chất hình thoi).