Câu hỏi:
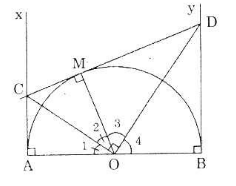
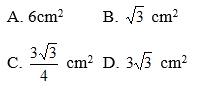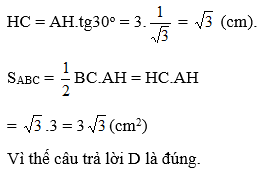09/07/2020 5,544Cho nửa đường tròn tâm O có đường kính AB (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi Ax, By là các tia vuông góc với AB (Ax, By và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ AB). Qua điểm M thuộc nửa đường tròn (M khác A và B), kẻ tiếp tuyến với nửa đường tròn nó cắt Ax và By theo thứ tự ở C và D. Chứng minh rằng:
a) ∠COD = 90o
b) CD = AC + BD
c) Tích AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OC là tia phân giác của ∠AOM
OD và tia phân giác của ∠BOM
OC và OD là các tia phân giác của hai góc kề bù ∠AOM và ∠BOM nên OC ⊥ OD.
=> ∠COD = 90o (đpcm)
b) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
CM = AC, DM = BC
Do đó: CD = CM + DM = AC + BD (đpcm)
c) Ta có: AC = CM, BD = DM nên AC.BD = CM.MD
ΔCOD vuông tại O, ta có:
CM.MD = OM2 = R2 (R là bán kính đường tròn O).
Vậy AC.BD = R2 (không đổi).
Hot: 500+ Đề thi vào 10 file word các Sở Hà Nội, TP Hồ Chí Minh có đáp án 2025 (chỉ từ 100k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
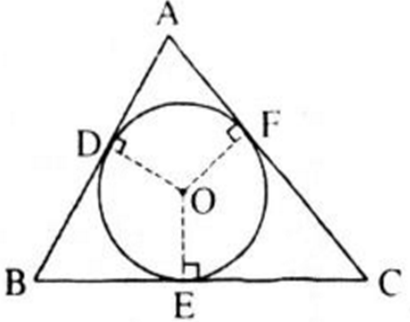
a) Theo tính chất của hai tiếp tuyến cắt nhau ta có:
BD = BE, CE = CF, AD = AF
Ta có:
AB + AC – BC = (AD + BD) + (AF + FC) – (BE + EC)
= (AD + AF) + (DB – BE) + (FC – EC)
= AD + AF = 2AD.
Vậy 2AD = AB + AC – BC (đpcm)
b) Tương tự ta tìm được các hệ thức:
2BE = BA + BC – AC
2CF = CA + CB – AB
Lời giải
- Chọn D.
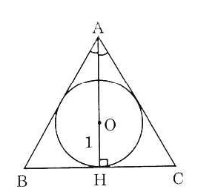
- Gọi O là tâm đường tròn nội tiếp Δ ABC, H là tiếp điểm thuộc BC.
Đường phân giác AO của góc A cũng là đường cao nên A, O, H thẳng hàng.
Ta có: HB = BC, ∠HAC = 30o, AH = 3.OH = 3 (cm)
Nhắn tin Zalo