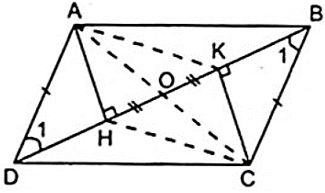
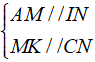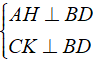Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD. Gọi O là trung điểm của HK. Chứng minh A, O, C thẳng hàng.
Câu hỏi trong đề: Tổng hợp lí thuyết và bài tập Toán 8 Chương 1: Tứ giác !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Áp dụng tính chất đường chéo của hình bình hành AHCK
Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường
Do O là trung điểm của HK nên O cũng là trung điểm của AC
⇒ A, O, C thẳng hàng.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
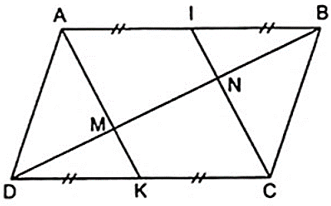
Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có:
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
⇒ DM = MN = NB
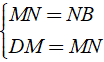
Lời giải
Từ giả thiết ta có:
⇒ AH//CK. ( 1 )
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
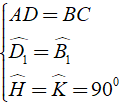
⇒ Δ ADH = Δ CBK
(trường hợp cạnh huyền – góc nhọn)
⇒ AH = CK (cạnh tương tứng bằng nhau) ( 2 )
Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo