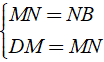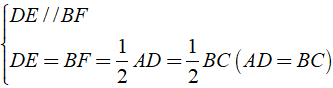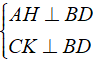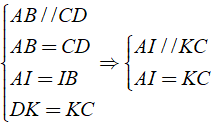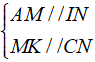Lý thuyết Bài 7: Hình bình hành
23 người thi tuần này 4.6 11.5 K lượt thi 5 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bài tập Tính diện tích xung quanh và thể tích của hình chóp tứ giác đều lớp 8 (có lời giải)
Bài tập Tính diện tích xung quanh và thể tích của hình chóp tam giác đều lớp 8 (có lời giải)
Bài tập Các bài toán thực tiễn gắn với việc vận dụng định lí Pythagore lớp 8 (có lời giải)
Bài tập Chứng minh các tính chất hình học lớp 8 (có lời giải)
Bài tập Tính độ dài cạnh trong tam giác vuông bằng cách sử dụng định lí Pythagore lớp 8 (có lời giải)
Danh sách câu hỏi:
Lời giải
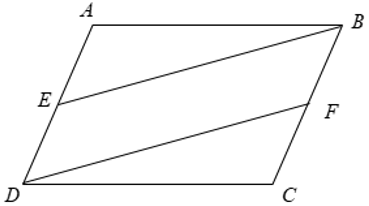
Xét tứ giác BEDF có
⇒ BEDF là hình bình hành
⇒ BE = DF (hai cạnh đối song song và bằng nhau)
Ta có: ABCD là hình bình hành nên
Lời giải
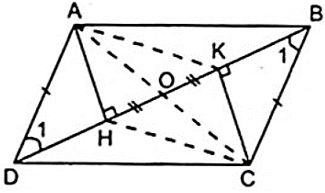
Từ giả thiết ta có:
⇒ AH//CK. ( 1 )
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
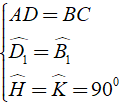
⇒ Δ ADH = Δ CBK
(trường hợp cạnh huyền – góc nhọn)
⇒ AH = CK (cạnh tương tứng bằng nhau) ( 2 )
Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
Lời giải
Áp dụng tính chất đường chéo của hình bình hành AHCK
Hình bình hành AHCK có hai đường chéo AC và HK cắt nhau tại trung điểm mỗi đường
Do O là trung điểm của HK nên O cũng là trung điểm của AC
⇒ A, O, C thẳng hàng.
Lời giải
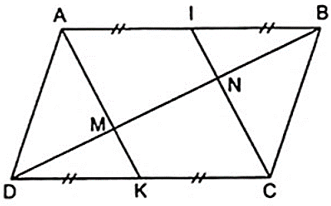
Áp dụng định nghĩa, tính chất và theo giả thiết của hình bình hành, ta có:
Tứ giác AICK có cặp cạnh đối song song và bằng nhau nên AICK là hình bình hành.
Lời giải
Theo câu a, AICK là hình bình hành
⇒ AK//CI. Khi đó , ta có:
Mặt khác, ta lại có: AI = IB, CK = KD theo giải thiết:
ÁP dụng định lý đường trung bình vào tam giác ABM, DCN ta có:
⇒ DM = MN = NB
Nhắn tin Zalo
Hỏi bài tập