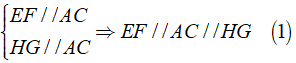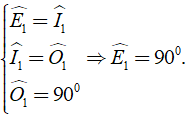Lý thuyết Bài 9: Hình chữ nhật
23 người thi tuần này 4.6 12 K lượt thi 3 câu hỏi
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Trắc nghiệm Mối liên hệ giữa xác suất thực nghiệm với xác suất và ứng dụng lớp 8 (có đáp án)
Trắc nghiệm Cách tính xác suất của biến cố bằng tỉ số lớp 8 (có đáp án)
Bài tập Nhận biết, chứng minh một tứ giác là hình chữ nhật lớp 8 (có lời giải)
Bài tập vận dụng tính chất hình chữ nhật lớp 8 (có lời giải)
Bài tập Nhận biết, chứng minh một tứ giác là hình bình hành lớp 8 (có lời giải)
Bài tập vận dụng tính chất hình bình hành lớp 8 (có lời giải)
Bài tập Nhận biết, chứng minh một tứ giác là hình thang, hình thang cân lớp 8 (có lời giải)
Danh sách câu hỏi:
Lời giải
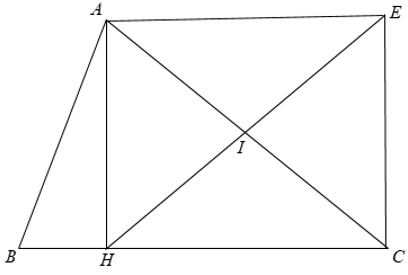
+ Trong Δ AHC vuông có I là trung điểm của AC
⇒ HE là đường trung tuyến của Δ AHC.
⇒ HI = 1/2AC = AI = IC.
Mà E đối xứng với H qua I ⇒ HI = IE.
Khi đó ta có HI = IE = AI = IC.
+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE
mà CI = 1/2HE ⇒ Δ HCE vuông tại C.
Tương tự xét với Δ AHE,Δ AEC đều là các tam giác vuông tại A, E.
Xét tứ giác AHCE có
⇒ AHCE là hình chữ nhật.
Lời giải
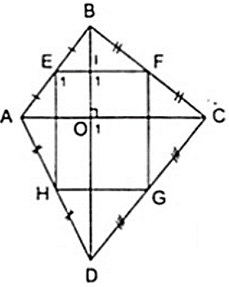
Tứ giác EFGH là hình chữ nhật.
Giải thích: Theo giả thiết ta có EF, GH lần lượt là đường trung bình của tam giác Δ ABC,Δ ADC
Áp dụng định lí đường trung bình vào hai tam giác ta được
Chứng minh tương tự: EH//FG//BD ( 2 )
Từ ( 1 ) và ( 2 ), tứ giác EFGH có hai cặp cạnh đối song song nên tứ giác EFGH là hình bình hành.
Gọi O là giao điểm của AC và BD, I là giao điểm của EF với BD.
Áp dụng tính chất của các góc đồng vị vào các đường thẳng song song ở trên và giả thiết nên ta có:
Hình bình hành EFGH có một góc vuông nên EFGH là hình chữ nhật.
Lời giải
Nhắn tin Zalo
Hỏi bài tập