Câu hỏi:

23/04/2022 589

Cho hình chóp \[S.ABCD\] có đáy là hình vuông tâm O, cạnh a, SO vuông góc với mặt phẳng \[\left( {ABCD} \right)\] và SO=a. Khoảng cách giữa SC và AB bằng:

A. $\frac{2 a \sqrt{5}}{5}$

B. $\frac{a \sqrt{3}}{15}$

C. $\frac{a \sqrt{5}}{5}$

D. $\frac{2 a \sqrt{3}}{15}$

Xem lời giải

Câu hỏi trong đề: [Năm 2022] Đề thi thử môn Toán THPT Quốc gia có đáp án (30 đề) !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Phương pháp giải:

- Sử dụng định lí: Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách từ đường thẳng này tới mặt phẳng song song và chứa đường thẳng kia.

- Đổi tính khoảng cách từ chân đường vuông góc với mặt phẳng, sử dụng công thức $A A^{'} \cap (P) = M \Rightarrow \frac{d (A; (P))}{d (A^{'}; (P))} = \frac{A M}{A^{'} M}$ .

- Dựng khoảng cách, sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.

Giải chi tiết:

$(VD): Cho hình chóp \[S.ABCD\] có đáy là hình vuông tâm O, cạnh a, vuông góc với mặt phẳng \[\left( {ABCD} \right)\] và . Khoảng cách giữa và bằng: (ảnh 6)$

Ta có $A B / / C D \Rightarrow A B / / (S C D) \supset S C$ $\Rightarrow d (A B; S C) = d (A B; (S C D)) = d (A; (S C D))$

Mà $A O \cap (S C D) = {C} \Rightarrow \frac{d (A; (S C D))}{d (O; (S C D))} = \frac{A C}{O C} = 2$ \[ \Rightarrow d\left( {A;\left( {SCD} \right)} \right) = 2d\left( {O;\left( {SCD} \right)} \right)\]

Gọi M là trung điểm của CD.

Vì OMlà đường trung bình của tam giác $A C D \Rightarrow O M / / A D \Rightarrow O M ⊥ C D$ và $O M = \frac{1}{2} A D = \frac{a}{2}$ .

Ta có: ${\begin{cases} C D ⊥ O M \\ C D ⊥ S O \end{cases} \Rightarrow C D ⊥ (S O M)$ .

Trong (SOM) kẻ $O H ⊥ S M (H \in S M)$ ta có: ${\begin{cases} O H ⊥ S M \\ O H ⊥ C D (C D ⊥ (S O M)) \end{cases} \Rightarrow O H ⊥ (S C D)$ .

$\Rightarrow d (O; (S C D)) = O H \Rightarrow d (A B; S C) = 2 O H$ .

Áp dụng hệ thức lượng trong tam giác vuông \[SOM\] ta có: $O H = \frac{S O . O M}{\sqrt{S O^{2} + O M^{2}}} = \frac{a . \frac{a}{2}}{\sqrt{a^{2} + \frac{a^{2}}{4}}} = \frac{a \sqrt{5}}{5}$ .

Vậy $d (A B; S C) = 2 O H = \frac{2 a \sqrt{5}}{5}$ .

Đáp án A.

Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

Bình luận

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hàm số y=f(x) có đạo hàm liên tục trên R. Biết hàm số y=f'(x) có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên $m \in [- 2021; 2021]$ để hàm số $g (x) = f (x + m)$ nghịch biến trên khoảng (1;2). Hỏi S có bao nhiêu phần tử?

A.2019

B.2022

C.2021

D.2020

Lời giải

Phương pháp giải:

- Tính g'(x).

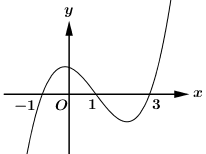
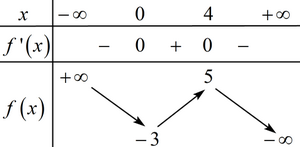
- Giải phương trình \[g'\left( x \right) = 0\], xác định số nghiệm của phương trình f'(x)=0 dựa vào đồ thị hàm số y=f'(x).

- Lập BXD đạo hàm g'(x) và suy ra các khoảng nghịch biến của hàm số.

- Để hàm số nghịch biến trên (1;2) thì (1;2) phải là con của những khoảng nghịch biến của hàm số.

Giải chi tiết:

Ta có: $g (x) = f (x + m) \Rightarrow g^{'} (x) = f^{'} (x + m)$ .

Cho $g^{'} (x) = 0 \Leftrightarrow f^{'} (x + m) = 0 \Leftrightarrow [\begin{array}{l} x + m = - 1 \\ x + m = 1 \\ x + m = 3 \end{array} \Leftrightarrow [\begin{array}{l} x = - 1 - m \\ x = 1 - m \\ x = 3 - m \end{array}$ .

Ta có \[g'\left( x \right) >0 \Leftrightarrow f'\left( {x + m} \right) >0\] \[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - 1 < x + m < 1}\\{x + m >3}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{ - 1 - m < x < 1 - m}\\{x >3 - m}\end{array}} \right.\].</></>

BXD g'(x):

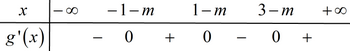
(VD): Cho hàm số có đạo hàm liên tục trên . Biết hàm số có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên để hàm số nghịch biến trên khoảng . Hỏi có bao nhiêu phần tử? (ảnh 18)

Để hàm số g(x) nghịch biến trên (1;2) thì $[\begin{array}{l} 2 \leq - 1 - m \\ 1 - m \leq 1 < 2 \leq 3 - m \end{array} \Leftrightarrow [\begin{array}{l} m \leq - 3 \\ 0 \leq m \leq 1 \end{array}$ .

Kết hợp điều kiện $m \in [- 2021; 2021], m \in ℤ$ $\Rightarrow m \in [- 2021; - 3] \cup [0; 1], m \in ℤ$ .

Vậy có 2021 giá trị nguyên của m thỏa mãn hay tập hợp S có 2021 phần tử.

Đáp án C.

Câu 2

Có bao nhiêu cách sắp xếp 8 học sinh thành một hàng dọc?

A. $7!$

B. $8^{8}$

C.8

D. $8!$

Lời giải

Phương pháp giải:

Sử dụng hoán vị.

Giải chi tiết:

Số cách sắp xếp 8 học sinh thành một hàng dọc là \[8!\] cách.

Đáp án D.

Câu 3

Gọi S là tập hợp tất cả các giá trị nguyên m để đồ thị hàm số $y = | 3 x^{4} - 8 x^{3} - 6 x^{2} + 24 x - m |$ có 7 điểm cực trị. Tính tổng các phần tử của S.

A.30

B.50

C.63

D.42

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 4

Tìm tập hợp tất cả các giá trị của tham số m để hàm số $y = \frac{1}{\sqrt{\log_{3} (x^{2} - 2 x + 3 m)}}$ có tập xác định là \[\mathbb{R}\].

A. $[\frac{2}{3}; 10]$

B. $(\frac{2}{3}; + \infty)$

C. $[\frac{2}{3}; + \infty)$

D. $(- \infty; \frac{2}{3})$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 5

Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y=m cắt đồ thị hàm số $y = x^{3} - 3 x^{2}$ tại ba điểm phân biệt A,B,C (B nằm giữa A và C) sao cho AB=2BC. Tính tổng các phần tử thuộc S.

A.0

B. $\frac{7 - \sqrt{7}}{7}$

C.-2

D.-4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 6

Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số $g (x) = f (4 x - x^{2}) + \frac{1}{3} x^{3} - 3 x^{2} + 8 x - \frac{5}{3}$ trên đoạn [1;3].

A.10

B.-10

C.9

D. $- \frac{5}{3}$

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

Cho giới hạn $\lim_{x \to - 4} \frac{x^{2} + 3 x - 4}{x^{2} + 4 x} = \frac{a}{b}$ , với \[\frac{a}{b}\] là phân số tối giản. Tính giá trị của biểu thức $a^{2} - b^{2}$ .

A. 9

B. -9

C. \[14\]

D. 41

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem thêm các câu hỏi khác »

Hỏi bài tập

Đăng ký gói thi VIP

VIP +1 tháng ( 199,000 VNĐ )

VIP +1 - Luyện thi tất cả các đề có trên Website trong 1 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +3 tháng ( 299,000 VNĐ )

VIP +3 - Luyện thi tất cả các đề có trên Website trong 3 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +6 tháng ( 399,000 VNĐ )

VIP +6 - Luyện thi tất cả các đề có trên Website trong 6 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

VIP +12 tháng ( 499,000 VNĐ )

VIP +12 - Luyện thi tất cả các đề có trên Website trong 12 tháng

Hơn 100K đề thi thử, đề minh hoạ, chính thức các năm
Với 2tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
Tải xuống đề thi [DOCX] với đầy đủ đáp án
Xem bài giảng đính kèm củng cố thêm kiến thức
Bao gồm tất cả các bậc từ Tiểu học đến Đại học
Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện

Mua ngay

Cho hình chóp \[S.ABCD\] có đáy là hình vuông tâm O, cạnh a, SO vuông góc với mặt phẳng \[\left( {ABCD} \right)\] và SO=a. Khoảng cách giữa SC và AB bằng:

Bình luận

Cho hàm số y=f(x) có đạo hàm liên tục trên R. Biết hàm số y=f'(x) có đồ thị như hình vẽ. Gọi S là tập hợp tất cả các giá trị nguyên m∈[−2021;2021] để hàm số g(x)=f(x+m) nghịch biến trên khoảng (1;2). Hỏi S có bao nhiêu phần tử?

Có bao nhiêu cách sắp xếp 8 học sinh thành một hàng dọc?

Gọi S là tập hợp tất cả các giá trị nguyên m để đồ thị hàm số y=|3x4−8x3−6x2+24x−m|có 7 điểm cực trị. Tính tổng các phần tử của S.

Tìm tập hợp tất cả các giá trị của tham số m để hàm số y=1log3(x2−2x+3m)có tập xác định là \[\mathbb{R}\].

Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y=m cắt đồ thị hàm số y=x3−3x2 tại ba điểm phân biệt A,B,C (B nằm giữa A và C) sao cho AB=2BC. Tính tổng các phần tử thuộc S.

Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số g(x)=f(4x−x2)+13x3−3x2+8x−53trên đoạn [1;3].

Cho giới hạn limx→−4x2+3x−4x2+4x=ab, với \[\frac{a}{b}\] là phân số tối giản. Tính giá trị của biểu thức a2−b2.

VIP +1 tháng ( 199,000 VNĐ )

VIP +3 tháng ( 299,000 VNĐ )

VIP +6 tháng ( 399,000 VNĐ )

VIP +12 tháng ( 499,000 VNĐ )

🔥 Đề thi HOT:

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đăng ký

Đăng nhập

Quên mật khẩu

Gọi S là tập hợp tất cả các giá trị nguyên m để đồ thị hàm số $y = | 3 x^{4} - 8 x^{3} - 6 x^{2} + 24 x - m |$ có 7 điểm cực trị. Tính tổng các phần tử của S.

Tìm tập hợp tất cả các giá trị của tham số m để hàm số $y = \frac{1}{\sqrt{\log_{3} (x^{2} - 2 x + 3 m)}}$ có tập xác định là \[\mathbb{R}\].

Gọi S là tập hợp tất cả các giá trị thực của tham số m để đường thẳng y=m cắt đồ thị hàm số $y = x^{3} - 3 x^{2}$ tại ba điểm phân biệt A,B,C (B nằm giữa A và C) sao cho AB=2BC. Tính tổng các phần tử thuộc S.

Cho hàm số y=f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số $g (x) = f (4 x - x^{2}) + \frac{1}{3} x^{3} - 3 x^{2} + 8 x - \frac{5}{3}$ trên đoạn [1;3].

Cho giới hạn $\lim_{x \to - 4} \frac{x^{2} + 3 x - 4}{x^{2} + 4 x} = \frac{a}{b}$ , với \[\frac{a}{b}\] là phân số tối giản. Tính giá trị của biểu thức $a^{2} - b^{2}$ .